Неявный метод Эйлера.

Пусть требуется численно решить систему обыкновенных дифференциальных уравнений

.

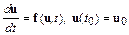Формально неявный метод Эйлера можно получить, рассматривая

,

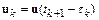где 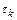– шаг интегрирования.

Разложим 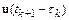в ряд Тейлора в окрестности точки :

.

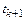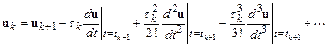Ограничившись в разложении двумя членами, придем к разностной схеме неявного метода Эйлера:

.

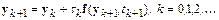Локальная погрешность при этом определяется отброшенными членами ряда Тейлора:

.

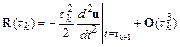Сравнивая явный и неявный методы Эйлера между собой (см. рис. 11.1), следует отметить, что методы обладают близкой по модулю, но разной по знаку погрешностью.

Рассмотрим устойчивость неявного метода Эйлера по отношению к шагу интегрирования. Применим его к системе уравнений

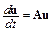
с отрицательно определенной матрицей 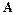, полагая шаг интегрирования 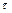постоянным:

.

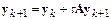Отсюда

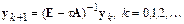
Пусть 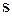– неособенная матрица, которая преобразованием подобия приводит матрицу 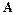к диагональному виду

.

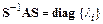Привлекая матрицу 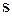, преобразуем итерационное правило следующим образом:

,

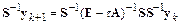или

,

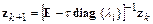где новая переменная

.

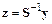Запишем результат для 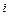-й компоненты вектора :

.

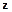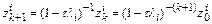Отсюда следует, что 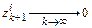при любом 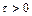, поскольку все .

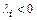Неявный метод Эйлера является абсолютно устойчивым по отношению к шагу интегрирования. При решении этим методом жестких систем дифференциальных уравнений шаг интегрирования выбирается только из соображений допустимой локальной погрешности.