Явный метод Эйлера.
Рассмотрим 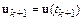 , где
, где 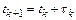 ,
, 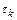 – текущий шаг интегрирования. Разложим функцию
– текущий шаг интегрирования. Разложим функцию 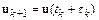 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 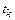 :
:
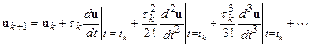 .
.
Ограничившись в этом разложении двумя членами, получим разност-ную схему метода Эйлера
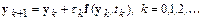 .
.
Локальная погрешность метода Эйлера составляет величину
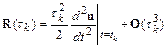 .
.
В вычислительной математике численные методы решения обык-новенных дифференциальных уравнений принято характеризовать порядком точности.
Определение. Если локальная погрешность численного метода 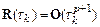 ,то порядок точности такого метода равен
,то порядок точности такого метода равен 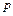 .
.
Метод Эйлера является методом первого порядка.
Приведем геометрическую интерпретацию явного метода Эйлера для задачи Коши
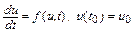
(см. рис. 10.2). Приращение на шаге интегрирования – катет прямоугольного треугольника, лежащий против угла, тангенс которого равен значению производной в предыдущий момент времени. Вторым катетом этого треугольника является текущий шаг интегрирования.
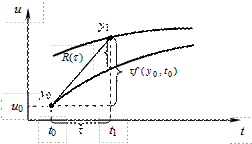
Рис. 10.2. Геометрическая иллюстрация явного метода Эйлера
Оценим устойчивость метода Эйлера по отношению к шагу ин-
тегрирования. Для этого рассмотрим линейную автономную систему
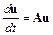
с отрицательно определенной 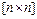 матрицей
матрицей 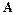 простой структуры. Отрицательная определенность матрицы означает, что все собствен-ные значения
простой структуры. Отрицательная определенность матрицы означает, что все собствен-ные значения 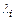 матрицы действительны и отрицательны, т. е.
матрицы действительны и отрицательны, т. е. 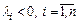 . В этом случае все решения
. В этом случае все решения 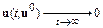 .
.
Применим для решения этой системы метод Эйлера с постоянным шагом 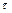 :
:
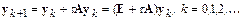 .
.
Здесь E –единичная матрица соответствующей размерности.
Из алгебры известно, что для любой неособенной матрицы 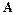 простой структуры существует такая неособенная матрица
простой структуры существует такая неособенная матрица 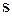 , которая преобразованием подобия приводит матрицу
, которая преобразованием подобия приводит матрицу 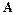 к диагональному виду:
к диагональному виду:
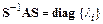 .
.
Преобразуем вычислительную схему метода Эйлера следующим образом:
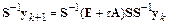 .
.
Введем замену переменных 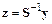 . Тогда
. Тогда
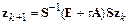 ,
,
или
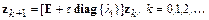 .
.
Запишем это соотношение для i-й компоненты вектора 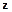 :
:
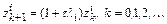 ,
,
или
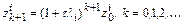 ,
,
где 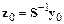 , т. е. определяется начальным условием.
, т. е. определяется начальным условием.
Нетрудно видеть, что
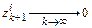 ,
,
если 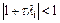 . Именно этим свойством обладает решение автономной системы с отрицательно определенной матрицей. Отсюда приходим к требованиям
. Именно этим свойством обладает решение автономной системы с отрицательно определенной матрицей. Отсюда приходим к требованиям
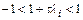 ,
,
при этом неравенство 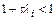 приводит к естественному условию
приводит к естественному условию 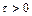 , т. к.
, т. к. 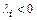 , а неравенство
, а неравенство 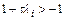 - к условию
- к условию
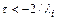 .
.
Очевидно, чтобы 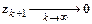 , необходимо при выборе шага интегрирования выполнить условие
, необходимо при выборе шага интегрирования выполнить условие
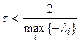 .
.
Таким образом, явный метод Эйлера по отношению к шагу интегрирования является условно устойчивым.
Явление жесткости.
Ограниченная устойчивость численного метода является серьезным недостатком при решении так называемых жестких систем.
Рассмотрим дифференциальное уравнение первого порядка
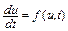 ,
,
для которого уравнение 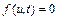 имеет единственное решение
имеет единственное решение
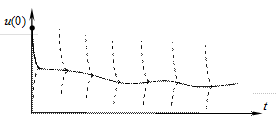
Рис. 10.3. К определению жесткости дифференциального уравнения
|
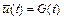 . Любая интегральная кривая такого дифференциального уравнения характеризуется двумя участками с существенно различным поведением решения (см. рис. 10.3), причем первый участок значительно меньше второго. Первый участок с быстрым изменением функции
. Любая интегральная кривая такого дифференциального уравнения характеризуется двумя участками с существенно различным поведением решения (см. рис. 10.3), причем первый участок значительно меньше второго. Первый участок с быстрым изменением функции 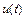 отражает стремление интегральной кривой к графику функции
отражает стремление интегральной кривой к графику функции 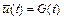 и называется пограничным слоем. На втором участке интегральная кривая практически совпадает с графиком
и называется пограничным слоем. На втором участке интегральная кривая практически совпадает с графиком 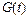 . Однако даже при небольшом отклонении от графика
. Однако даже при небольшом отклонении от графика 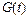 в любой его точке производная
в любой его точке производная 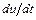 резко возрастает по сравнению с производной
резко возрастает по сравнению с производной 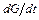 . Именно по этой причине малый шаг интегрирования, используемый при воспроизведении быстропротекающего участка, не может быть существенно увеличен вне пограничного слоя в явных методах численного интегрирования.
. Именно по этой причине малый шаг интегрирования, используемый при воспроизведении быстропротекающего участка, не может быть существенно увеличен вне пограничного слоя в явных методах численного интегрирования.
Рассмотрим примеры жестких систем.
1. Простейшее дифференциальное уравнение
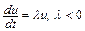 (10.1)
(10.1)
может быть жестким (рис. 10.4) , если интервал наблюдения 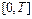 зна-
зна-
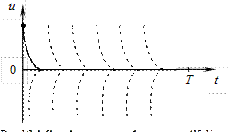
Рис. 10.4. Семейство решений уравнения (10.1)
чительно превосходит величину 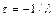 . Решением такого уравнения является функция
. Решением такого уравнения является функция 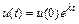 . Пунктирные линии на рис. 10.4 соответствуют различным значениям
. Пунктирные линии на рис. 10.4 соответствуют различным значениям 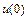 .
.
2. Для иллюстрации явления жесткости дифференциальных уравнений может быть полезной также любая система линейных ОДУ, матрица которой характеризуется большим разбросом собственных значений, например система
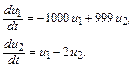 (10.2)
(10.2)
Здесь собственные числа матрицы есть 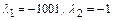 .
.
Решение этой системы (рис. 10.5)
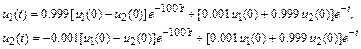
содержит быструю составляющую как для 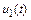 , так и для
, так и для 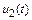 , хотя по амплитуде быстрая составляющая функции
, хотя по амплитуде быстрая составляющая функции 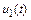 значительно превосходит аналогичную компоненту функции
значительно превосходит аналогичную компоненту функции 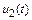 (ее на рис. 10.5 в таком масштабе отобразить не удалось).
(ее на рис. 10.5 в таком масштабе отобразить не удалось).
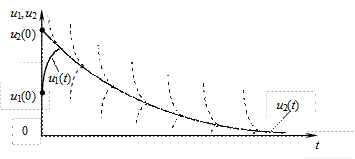
Рис. 10.5. Решение жесткой системы ОДУ (10.2)
Завершая краткую характеристику свойства жесткости дифференциальных уравнений, отметим, что при решении научных задач жесткость уравнений является скорее правилом, чем исключением. По этой причине для таких задач разработаны специальные методы численного интегрирования.
Лекция 11
Одношаговые методы
ЦЕЛЬ ЛЕКЦИИ: Построить простейший неявный одношаговый метод, обладающий свойством устойчивости к шагу интегрирования, оценить его локальную погрешность; дать способ Рунге–Кутта увеличения точности одношаговых методов, проиллюстрировав его методами второго и четвертого порядков точности; привести разностную схему линейных многошаговых методов, получить условия корректного выбора коэффициентов.
Дата добавления: 2015-11-24; просмотров: 2325;
