Интегрирование уравнений Эйлера. Уравнение Бернулли
Когда массовыми силами являются только силы тяжести, то
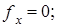
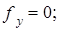
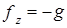
и уравнение (12) сводится к
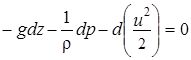 .
.
Интегрирование дает
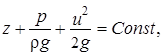 (13)
(13)
где z – отметка центра живого сечения струйки над плоскостью сравнения 0-0 (геометрическая высота);
р/rg – пьезометрическая высота, соответствующая гидродинамическому давлению в этой точке;
u²/2g – высота скоростного напора.
Уравнение (13) для элементарной струйки идеальной жидкости было получено Даниилом Бернулли в 1738 г. и носит его имя. Через год такой же результат опубликовал отец Бернулли. Вопрос о приоритете так и не был решен между ними.
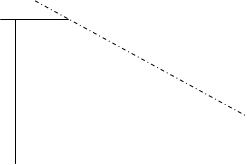
Геометрический смысл уравнения Бернулли иллюстрируется рис.28. В отличие от гидростатики пьезометрическая линия Р-Р не является горизон-тальной прямой. Напорная линия Е-Е, получаемая суммированием перечис-ленных высот, параллельна плоскости сравнения.
Энергетическая форма уравнения Бернулли имеет вид
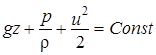 ,
,
где gz – удельная потенциальная энергия положения;
p/r – удельная потенциальная энергия давления;
u²/2 – удельная кинетическая энергия струйки.



 E E
E E
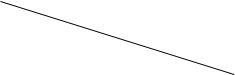 u1/2g
u1/2g
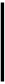

 P u2/2g
P u2/2g
 p1/ρg
p1/ρg


 P
P
 p2/ρg
p2/ρg
 |


 z1
z1
z2
 0 0
0 0
Рис.28
Таким образом, уравнение Бернулли является частным случаем закона сохранения энергии применительно к установившемуся движению элемен-тарной струйки идеальной жидкости. Оно распространяется и на поток идеальной жидкости в каналах конечных размеров, так как все элементарные струйки имеют одинаковую скорость и, следовательно, v=u
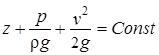 .
.
Дата добавления: 2015-11-26; просмотров: 1368;
