Групповые методы для уравнений динамики нити.

Рассмотрим проекцию уравнений движения упругой нити на естественные оси:

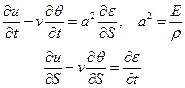
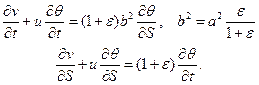
Введём безразмерные переменные и искомые функции

.

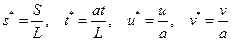В новых обозначениях (звёздочки опустим для сокращения записи) уравнения примут следующий вид

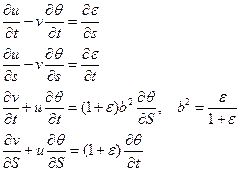
Применим преобразование растяжения сжатия ко всем переменным системы

.

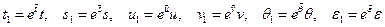Запишем уравнения для новых переменных

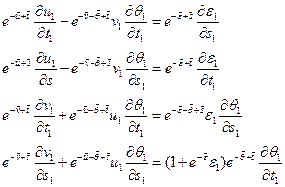
Потребуем, чтобы уравнения были инвариантны относительно преобразований растяжения (сжатия). В результате получим систему уравнений

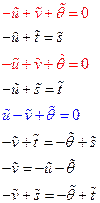
Из последней системы следует, что , .

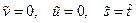Получилась очень бедная группа преобразований. Она допускает всего одно инвариантное преобразование 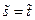. Единственно возможной комбинацией независимых переменных, которая допускается данной группой, является отношение

.

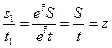Проверка показывает, что автомодельное решение существует

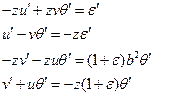
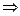
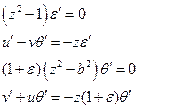
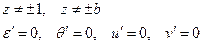
То есть, мы получили уже известное нам решение.

Рассмотрим в качестве примера более нетривиальную систему уравнений

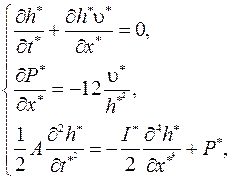
Выпишем общий вид преобразования растяжения-сжатия зависимых и независимых переменных системы уравнений (1.28)(примечание: индексом 1 помечены преобразованные величины):

,

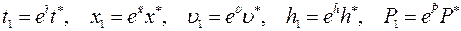где 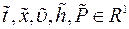- групповые параметры искомой однопараметрическойподгруппы преобразований.

Требование инвариантности системы уравнений относительно преобразований приводит к определенным связям между этими групповыми параметрами.

Исходя из этого, получим следующую систему уравнений:

Откуда .

В результате мы получили однопараметрическую группу преобразований растяжения (сжатия), допускаемую системой уравнений

.

Найдем такие комбинации переменных, которые не меняются (остаются инвариантными) при любых значениях группового параметра 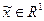. Нетрудно заметить, что независимые переменные в комбинации

являются инвариантными при любых значениях .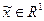

Таким образом, автомодельное решение следует искать в виде

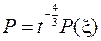
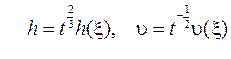
где 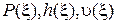некоторые функции от переменной 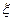. Они удовлетворяют следующей системе уравнений

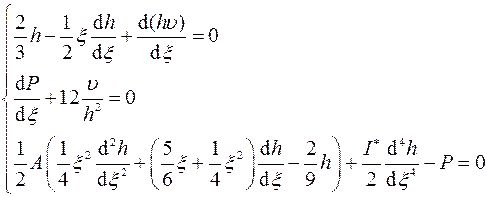
Таким образом, автомодельная задача сведена к решению системы из трех обыкновенных дифференциальных уравнений. Конкретный вид искомых функций определяется граничными условиями решаемой задачи. Однако, даже не решая систему, мы можем видеть тенденцию поведения решения во времени

, .

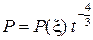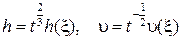Вопросы для самоконтроля.При сдаче экзамена или зачета требуется владеть основными теоретическими фактами математической модели нити. Для этого полезно продумать ответы на следующие вопросы:

- Какие волны могут распространяться в упругой растяжимой нити?

- Какой тип будет иметь система уравнений движения нерастяжимой нити?

- Что можно сказать о величинах скоростей продольных и поперечных волн слабого разрыва в упругой нити при их сравнении?

- Может ли величина скорости поперечных волн быть больше величины скорости продольных волн в случае нелинейно упругого материала?

-Что дает сравнение величин для скоростей волн сильного и слабого разрыва (продольных и поперечных)?

- Какой характер будет носить движение в недеформированной, прямолинейной, покоящейся, бесконечной упругой нити, если одна из её точек начнет двигаться с постоянной скоростью?