Волны в идеальной растяжимой нити

Математическая модель гибкой нити.Идеальной нитью будем считать тело, у которого два характерных линейных размера пренебрежимо малы по сравнению с третьим, что позволяет описывать движение такого тела, как движение некоторой математической кривой, совпадающей со срединным волокном тела (срединное волокно – кривая, состоящая из точек, которые являются геометрическими центрами тяжести нормальных сечений тела). При этом главный вектор сил в каждом сечении тела, перпендикулярном срединному волокну, во все моменты времени направлен по нормали к рассматриваемому сечению или, иначе говоря – по касательной к срединному волокну. Момент сил, действующих в рассматриваемом нормальном сечении, предполагается равным нулю (Рис.1).

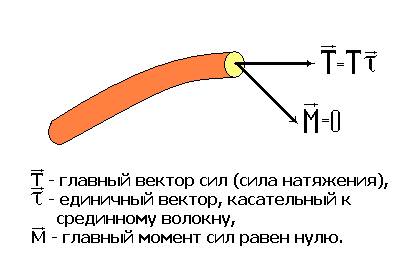
Рис.1

Главный вектор сил в сечении тела, перпендикулярном срединному волокну, называется силой натяжения. Обозначим эту силу как .

В нерастянутом состоянии каждой точке срединного волокна можно поставить в соответствие некоторое значение – по абсолютной величине это длина дуги срединного волокна, отсчитываемая от выбранной точки в выбранном направлении, знак выбирается в зависимости от выбранного направления. Таким образом, мы каждой материальной точке нити фактически присваиваем имя – её дуговую координату в недеформированном состоянии. Это означает, что изучение движения нити сводится к определению поведения во времени радиуса – вектора 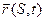каждой материальной точки срединного волокна нити (Рис.2).

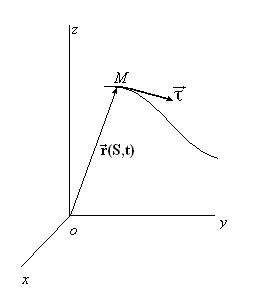
Рис.2

Если нить растяжима, то длина дуги между двумя материальными точками может меняться. Введем дуговую координату 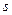, как длину дуги в растянутом состоянии с тем же правилом выбора знака, что и для дуги 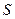. Тогда для двух различных последовательно расположенных материальных точек нити можно рассматривать две величины: 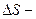длина дуги 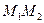в нерастянутом состоянии; 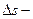длина дуги 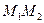в текущем, т.е. растянутом состоянии.

Тогда можно определить относительное удлинение нити

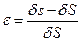. (3.1)

Единичный вектор, касательный к нити, вычисляется как предел отношения приращения её радиуса 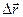вектора к своей длине 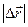. Но эта длина совпадает по определению с текущей длиной дуги, т.е. 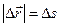.Поскольку из (1) следует связь приращений начальной и текущей дуговых координат

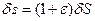, можно определить единичный вектор касательной следующим выражением

.

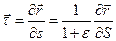Отсюда получается выражение производной радиуса – вектора по начальной дуговой координате

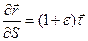. (3.2)

Скорость 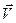и ускорение 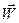материальных точек нити вычисляется в виде соответствующих частных производных радиуса – вектора по времени

( поскольку для конкретной материальной точки дуговая координата 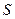фиксирована)

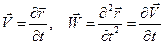. (3.3)

Для нити можно ввести линейную плотность в нерастянутом состоянии

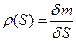
и аналогичную плотность в текущем, т.е. растянутом состоянии

.

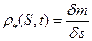Поскольку в обоих определениях плотности масса 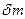соответствует одному и тому же малому участку материального волокна, в силу закона сохранения массы и определения деформации (3.1) отсюда следует соотношение между двумя введенными плотностями

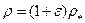. (3.4)

Фактически уравнение (3.4) является записью закона сохранения массы для нити. Это уравнение позволяет при необходимости определить текущую плотность нити при помощи начальной. Это возможно сделать, если мы знаем распределение деформации в данный момент времени.

Запишем закон изменения количества движения для произвольного выделенного участка нити 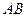(точка 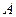имеет дуговую координату 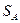, а точка 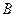– координату 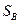). Для этого обозначим плотность внешних массовых сил величиной 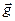, а линейную плотность результирующей внешних поверхностных сил, действующих на боковой поверхности нити, величиной 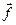(Рис.3).

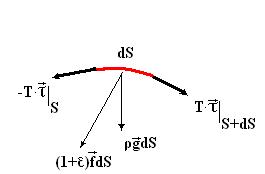
Рис.3

Тогда закон изменения количества движения можно представить в следующей форме

.

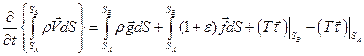Если перенести все члены выписанного равенства в левую часть, то оно может быть представлено в виде

.

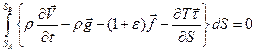Поскольку пределы интегрирования произвольны, то, если потребовать непрерывности функции, стоящей в фигурных скобках, она должна быть тождественно равна нулю. Таким образом, мы приходим к следующему дифференциальному уравнению движения нити

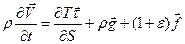. (3.5)

К данному динамическому уравнению движения присоединим кинематическое уравнение, следующее из дифференциального тождества 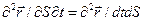. Если учесть выражение (3.3) для скорости и соотношение (3.2), то из равенства смешанных производных радиуса – вектора 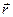получим

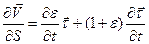. (3.6)

Система уравнений (3.5), (3.6) вместе с условием единичности вектора 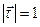касательной к нити не является замкнутой для искомых функций 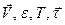. Как и все модели сплошных сред, рассматриваемая модель нити замыкается феноменологической связью между натяжением и деформацией, т.е. как и следовало ожидать свойствами материала, из которого изготовлена сама нить. Мы будем считать эту связь упругой. Тогда к системе уравнений следует присоединить уравнение состояния в виде однозначной связи между действующим натяжением и возникающей вследствие этого деформацией

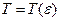. (3.7)

Для некоторых задач эта связь может быть еще более простой, когда зависимость натяжения от деформации считается линейной

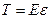. (3.8)

Следует помнить о том, что модуль упругости 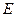имеет в линейно упругом случае (3.8) размерность силы натяжения.

Для исследования и решения уравнений (3.5) –(3.6) необходимы их проекции на выбранные направления. Наиболее простую и удобную для наших целей форму имеют проекции этих уравнений на т.н. естественные подвижные оси, базисом которых для каждой точки нити является набор единичных векторов

,

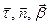где 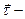единичный вектор, касательный к нити, 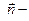единичный вектор нормали к соприкасающейся с нитью окружности, 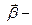единичный вектор бинормали. Если ограничиться рассмотрением плоского движения, то достаточно рассматривать два направления – касательное и нормальное.

Пусть нить двигается в плоскости 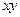декартовой системы координат наблюдателя (Рис.4). Обозначим величиной 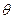угол, который составляет касательная с осью 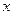в рассматриваемой точке нити. Тогда вектор касательной и нормали задаются этим углом

,

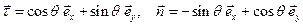а дифференциалы этих векторов связаны соотношениями

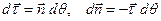. (3.9)

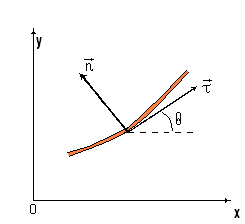
Рис.4.

Если представить вектор скорости в подвижном базисе 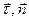разложением

и спроектировать уравнения (3.5), (3.6) на подвижные оси, то с учетом (3.9) получим:

в проекции на направление – 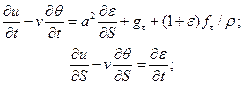(3.10)

в проекции на направление 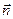– 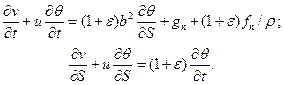(3.11)

В уравнениях (3.10), (3.11) введены величины

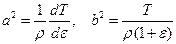, (3.12)

имеющие размерность скорости, а также учтено уравнение состояния (3.7). Геометрическая интерпретация введенных величин, представленная на Рис.5, позволяет сказать, что для диаграмм (3.7) с выпуклостью одного знака, максимум величин 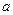всегда больше максимума .

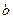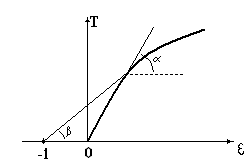
Рис.5. Геометрическое представление для квадратов скоростей

.

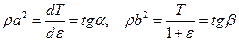Нашей задачей является изучение распространения волн в нити.

Волны в нити. Рассмотрим некоторую кривую в пространстве независимых переменных 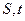. Под волнами или малыми возмущениями обычно (но не всегда) понимается распространение слабых разрывов искомых функций по пространству во времени. В нашем случае вдоль рассматриваемой кривой будут распространяться слабые разрывы тогда, когда на ней непрерывны сами искомые функции, но терпит разрыв хотя бы одна их производная по времени или координате 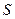. Такие кривые, если они существуют, называют характеристиками. Если количество характеристик совпадает с количеством уравнений решаемой системы первого порядка, такая система уравнений называется гиперболической. Одним из самых интересных свойств характеристических линий является то, что вдоль них уравнения системы можно записать в полных дифференциалах. По сути, и сами характеристики можно искать как линии, вдоль которых уравнения можно представить в полных дифференциалах.

Поскольку учет массовых сил и внешних сил сопротивления принципиально не изменяет сути, но делает выкладки значительно более громоздкими, рассмотрим уравнения (3.10), (3.11) при отсутствии выше перечисленных сил.

В этом случае пара уравнений (3.10) может быть легко записана в полных дифференциалах. Действительно, умножим первое уравнение (3.10) на 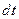, второе – на дифференциал 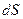и сложим, полученные равенства. В результате получим

.

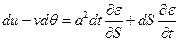Из данного равенства можно получить и сами характеристики и уравнения, которые вдоль них выполнены, если искать связь 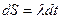с неизвестным коэффициентом 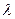из того условия, что правая часть равенства должна быть записана в виде полного дифференциала. Исходя из этого требования, немедленно получаем, что такие линии есть 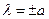и вдоль них выполнены уравнения 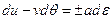. Аналогичные выкладки можно проделать и с парой уравнений (3.11). Таким образом, можно получить для нити четыре характеристики, вдоль которых должны быть выполнены соответствующие соотношения в полных дифференциалах:

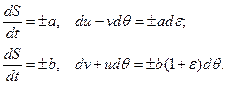(3.13)

Те же линии мы получим и в том случае, когда будем искать их как линии слабого разрыва. В этом случае, применяя операцию скачка для уравнений (3.10), (3.11) и для полных дифференциалов вдоль пока неизвестных линий, получим систему восьми уравнений для скачков производных искомых функций (следует помнить, что скачки их приращений равны нулю в силу непрерывности самих функций). Полученная система уравнений однородна. Исходя из определения характеристики, на ней должен отличаться от нуля хотя бы один из скачков производных. Отсюда следует, что однородная система должна иметь отличное от нуля решение. А это возможно только в том случае, когда равен нулю её определитель. В результате мы должны получить уравнения всех возможных характеристических линий. Покажем, что они совпадают с уже найденными кривыми. Ниже приведены основные действия, которые были перечислены выше.

Система для скачков производных 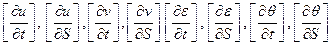, взятых именно в таком порядке, имеет следующую матрицу

.

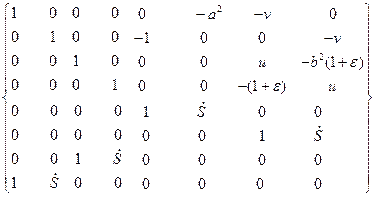После приведения матрицы к треугольному виду, получим

.

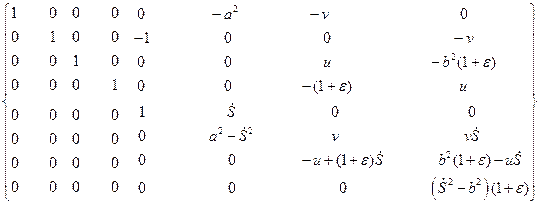Откуда найдем значение определителя. Приравнивая его нулю, имеем

.

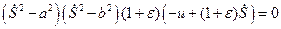Отсюда следуют все возможные значения для скоростей слабого разрыва

.

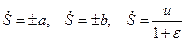Примем 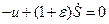, тогда получим из уравнений системы (3.10), (3.11)

.

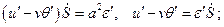
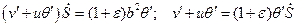В этом случае скорость движения возмущений по растянутой нити равна 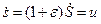, т.е. совпадает со скоростью самих точек нити. Поскольку выбор системы координат определяется наблюдателем, выберем её так, чтобы скорость 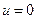. Тогда и полученная скорость 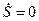также равна нулю, т.е. возмущения переносятся в пространстве, но не переносятся по точкам нити.

Подстановка 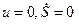приводит к системе уравнений

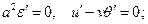
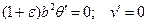
с тривиальным решением 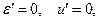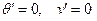, которое означает отсутствие каких либо возмущений. Это означает, что данное значение скорости возмущений является физически посторонним решением и не реализуется.

Волны сильного разрыва в нити. Рассмотрим возможность распространения по нити волн сильного разрыва, когда на фронте волны терпит разрыв хотя бы одна из искомых функций. В этом случае необходимо записать закон изменения импульса в интегральной форме. Введем скорость движения фронта сильного разрыва по материальным точкам нити 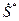и рассмотрим элемент нити 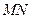длины 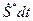, который за промежуток времени 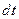переходит с одной (невозмущенной) стороны фронта (0) на другую (возмущенную) сторону (1) (Рис.6).

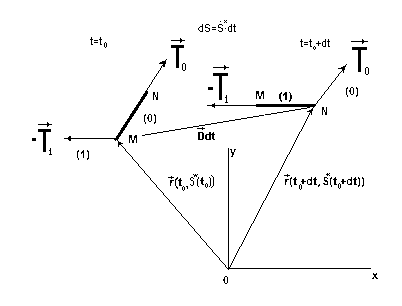
Рис.6.

При этом в пространстве 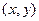наблюдателя за время 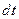фронт перемещается на вектор 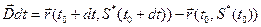. Тогда для абсолютной скорости фронта в системе координат 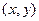справедливо кинематическое равенство

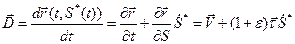. Поскольку вычисление скорости движения фронта не должно зависеть от того, с какой стороны фронта мы это вычисление делаем, скачек правой части данного равенства должен быть равен нулю

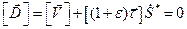. (3.14)

Закон изменения количества движения для рассматриваемого материального элемента 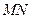приводит к равенству 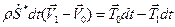. Отсюда следует еще одно уравнение на сильном разрыве в нити

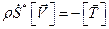. (3.15)

Для вектора касательной к нити есть только две возможности – иметь разрыв или быть непрерывным. Рассмотрим каждую из этих возможностей отдельно.

Допустим, что вектор 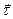не меняется при переходе через фронт сильного разрыва. Тогда с учетом этого факта уравнения (3.14), (3.15) можно переписать в форме

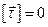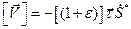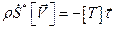, , . (3.16)

В плоском случае из (16) получим:

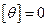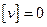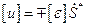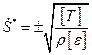, , , . (3.17)

В случае линейно упругого материала нити 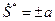. Т.е. в этом случае продольные волны сильного разрыва распространяются с той же скоростью, что и продольные волны слабого разрыва.

Осталось рассмотреть случай, когда вектор касательной меняется при переходе через фронт сильного разрыва. Тогда условия (3.14), (3.15) приводят к векторному равенству

.

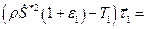
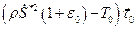Это равенство возможно только в случае равенства нулю коэффициентов при единичных векторах, т.е.

,

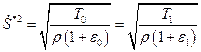откуда следует непрерывность деформации. Учитывая этот факт, условия на поперечной волне сильного разрыва можно представить в следующем виде:

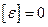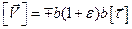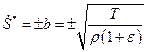, , . (3.18)

В отличие от предыдущего случая, поперечные волны сильного и слабого разрыва всегда имеют одинаковую скорость независимо от того, является материал нити линейно упругим или нет. В случае линейно упругого материала нити .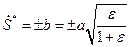

Плоское автомодельное движение нити.Допустим, что нить линейно упруга и бесконечна. В начальный момент времени она покоится, но имеет разные постоянные значения деформации 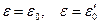и угла наклона 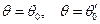в каждой из двух областей. Требуется определить свободное движение нити в последующие моменты времени при отсутствии сил сопротивления и массовых сил. Из Пи-теоремы теоремы следует, что все безразмерные искомые функции должны зависеть от безразмерных параметров задачи. В нашей задаче искомые функции

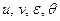
зависят от следующего набора параметров

.

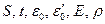Отсутствие характерного линейного размера дает возможность на единицу уменьшить число независимых переменных и искать автомодельное решение от переменной 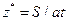. Для размерной формы уравнений можно искать решение от переменной 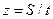. В этом случае запись дифференциальных операторов будет такой

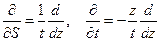. (3.19)

При отсутствии массовых сил и сопротивления движению нити уравнения (3.10), (3.11) в автомодельном случае приводятся к виду

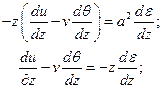(3.20)

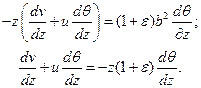(3.21)

Из уравнений (3.20) следует, что

,

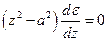а из уравнений (3.21) –

.

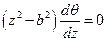Эти условия позволяют сделать следующий вывод. Если независимая переменная удовлетворяет условиям 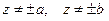, все искомые производные равны нулю, т.е. решением является набор постоянных значений искомых функций

.

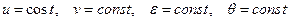Сами значения могут быть разными по разные стороны от особых точек решения . Дифференциальные уравнения не позволяют найти эти постоянные значения, поскольку в особых точках терпят разрыв сами искомые функции. Таким образом, автомодельное решение соответствует распространению волн сильного разрыва в областях с постоянными значениями всех параметров задачи. Области (0) и (0’) на рис.7 соответствуют начальным значениям задачи, области (1) и (1’) – тем областям, куда уже добежали продольные волны сильного разрыва. Область (2) – область тех точек, до которых добежали и продольные и поперечные волны. Отметим, что на продольном фронте должны выполняться условия (3.17), а на каждом поперечном фронте – условия (3.18). Для заданной нити (плотность и модуль упругости) и заданных начальных условиях задача определения решения замкнута (система 12 уравнений с 12 неизвестными). На кадре, сделанном высокоскоростной камерой (Рис.8), визуально видна реализация автомодельного движения в эксперименте.

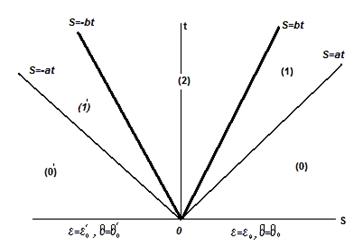
Рис.7

Рис.8