ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ЭЙЛЕРА

Пусть вектор f имеет потенциал, т.е. существует такая функция U(x, у, z), что

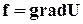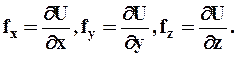или (2.3.1)

При этом уравнение (2.2.4) для однородной несжимаемой жидкости (р = const) примет вид

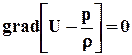. (2.3.2)

Интеграл уравнения (2.3.2) дает равенство

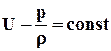, (2.3.3)

которое представляет собой общую форму интеграла уравнений гидро­статики, когда объемные силы имеют потенциал. Если внешние объем­ные силы не имеют потенциала, то в поле таких сил жидкость не может находиться в состоянии покоя.

Рассмотрим частные случаи объемных сил.

Внешняя объемная сила - сила тяжести. Пусть в декартовой систе­ме координат ось z направлена вверх. Используя (2.3.1), установим, что потенциал силы тяжести:

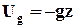, (2.3.4)

где g - ускорение свободного падения, при этом

.

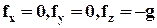Подставим (2.3.4) в (2.3.3):

.

Обозначив через g удельный вес (g = rg), получим:

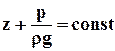или 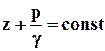. (2.3.5)

Это закон распределения гидростатического давления в поле силы

тяжести. Обозначим через р₀ давление на свободной поверхности, или поверхностное давление, и найдём форму свободной поверхности из условия, что на ней р = р₀ = const. Из (2.3.5) следует, что такая поверхность, координаты которой обозначим через z₀, представляет собой горизонтальную плоскость:

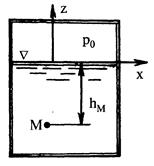Рис.2.3. Гидростатическое давление в поле силы тяжести

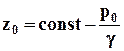. (2.3.6)

Определённое таким образом давление называется абсолютным давлениеми обозначается через р_А. Представим на рис. 2.3 замкнутый сосуд, ча­стично заполненный жидкостью. Давление на сво­бодной поверхности равно р₀. Если h_M – это рас­стояние от свободной поверхности до точки М (заглубление точки), а начало координат распо­ложено на свободной поверхности, так что h_M = -z (рис. 2.3), то в точке М абсолютное давление

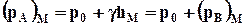, (2.3.7)

где р_в = gh - весовоедавление, т.е. давление, обусловленное весом жид­кости.

Обычно в технических приложениях используют не абсолютноедав­ление р_А, а его отклонение от атмосферногодавления р_а. Если Р_А > Р_а, то избыточнымдавлением р_и называется превышение давления в точке над атмосферным:

р_{и =} р_А– р_а. (2. 3.8)

Если на свободную поверхность действует атмосферное давление, то весовое давление в жидкости равно избыточному, и абсолютное давление в любой точке внутри жидкости согласно (2.2.7) можно записать в виде

р_а = Р₀ + Р_в = Р_а + gh = Р_а + Р_и . (2. 3.9)

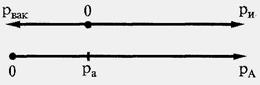Рис.2.4. Пояснения к определению избыточного и вакуумного давлений

При условии Р_А < р_а недостаток давления в точке до атмосферного называется вакуумом:

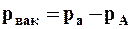. (2.3.10)

Введённые выше определения избыточного давления р_и и давления вакуума р_вак представлены на рис. 2.4 в виде переноса начала отсчёта давления в точку р_а.