ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ (УРАВНЕНИЕ ЭЙЛЕРА)

В пространстве, заполненном движущейся идеальной жидкостью плотностью 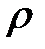, выделим элементарный параллелепипед, ребра которого со сторонами 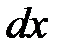, , 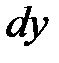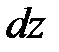параллельны осям координат (рис. 3.9). При движении идеальной жидкости отсутствуют силы внутреннего трения. Элементарный объем, находящийся в параллелепипеде, перемещается с абсолютной скоростью 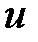. Составляющие этой скорости по осям координат будут , , .

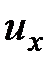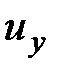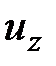На элементарный объем будут действовать массовые и поверхностные силы. Силы трения при движении параллелепипеда равны нулю.

Масса жидкости в элементарном объеме параллелепипеда

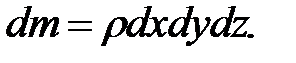(3.52)

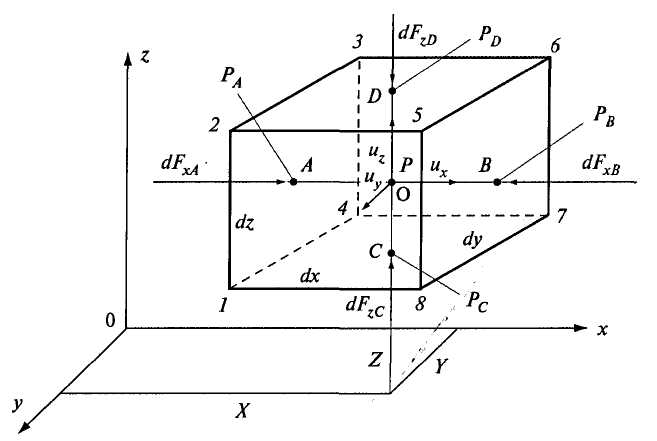
Рис. 3.9. К выводу уравнения движения Эйлера

Проекции массовых сил в направлении координатных осей:

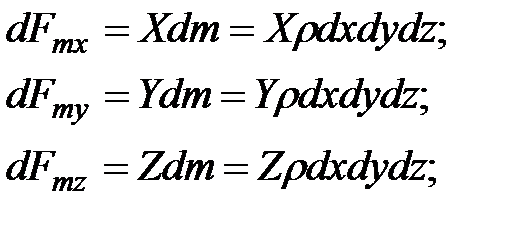(3.53)

где 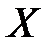, , 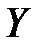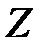- компоненты единичных массовых сил относительно осей 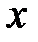, , 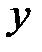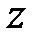(проекции ускорения этих сил).

Поверхностные силы определяются давлением, приходящимся на грани параллелепипеда.

Пусть в центре тяжести параллелепипеда (т. О) гидростатическое давление равно 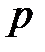, координаты этой точки 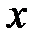, , 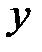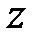. Скорость движения в этой точке 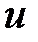. Составляющие этой скорости по осям координат равны , , .

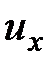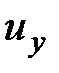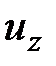Проведем через т. О горизонтальную линию, параллельную оси 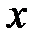. Точки пересечения с гранями параллелепипеда А (грань 1234), В (грань 5678). Давление в этих точках по оси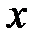 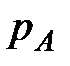и .

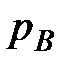В жидкой сплошной среде давление в точке выражается непрерывной сплошной функцией координат расположения точки в пространстве: 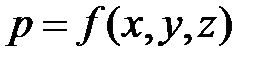. Гидростатическое давление изменяется непрерывно линейно, и приращение давления на единицу элементарной длины - - -

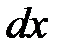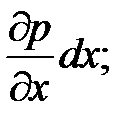
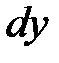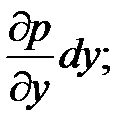
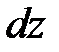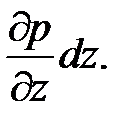
Следовательно, давления в точках А и В будут различаться на величину .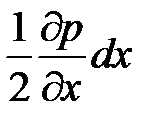

Давления в точках А и В выразим в следующем виде:

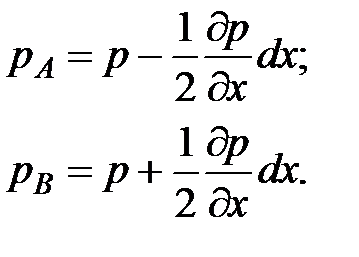(3.54)

Из-за малости площади граней можно считать, что давления 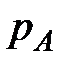и 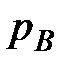являются средними гидростатическими давлениями, действующими на грани 1234 и 5678. Поверхностные силы давления на эти грани по оси 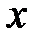равны произведению давления на площади граней:

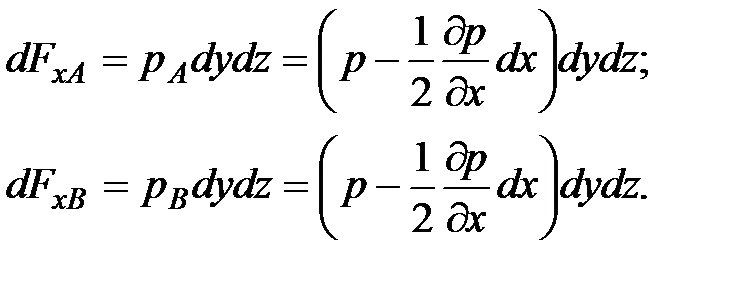(3.55)

Аналогично поверхностные силы давления на грани по оси z (грани 1478и 2365):

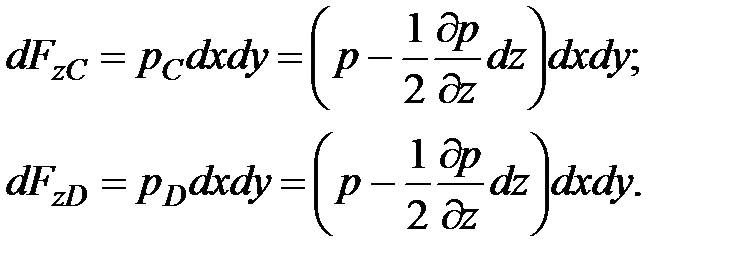(3.56)

Также можно определить поверхностные силы на грани по оси .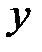

Рассмотрим равновесие параллелепипеда, находящегося в движущейся жидкости, используя принцип Даламбера.

Согласно принципу Даламбера уравнение движения можно рассматривать как уравнение равновесия, если ввести силы инерции. Полагаем, что параллелепипед массой 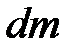перемещается со скоростью 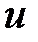, составляющие этой скорости , , .

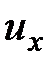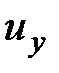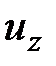Сила инерции 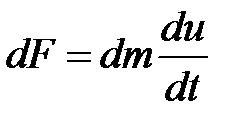( 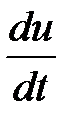- ускорение).

Проекции силы инерции на соответствующие координатные оси:

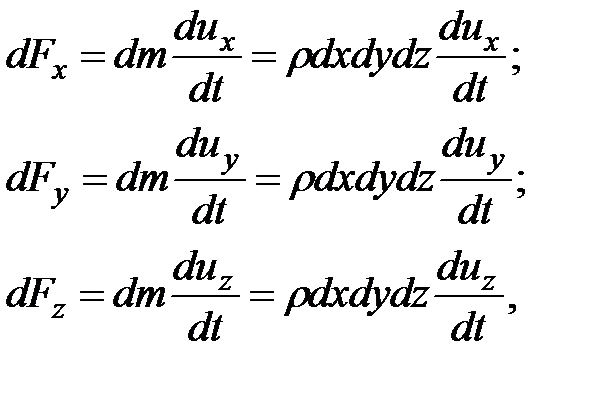(3.57)

где 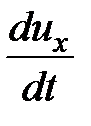, , 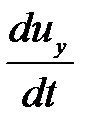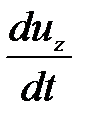- проекции ускорении на оси , , .

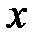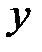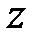Составим уравнение равновесия для сил, действующих на рассматриваемый параллелепипед жидкости, с учетом силы инерции по осям 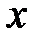и :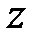

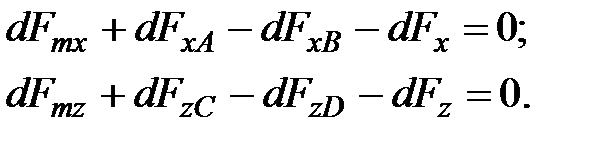(3.58)

Подставляя в (3.58) полученные ранее зависимости (3.53), (3.55), (3.56) и (3.57), получим следующие уравнения

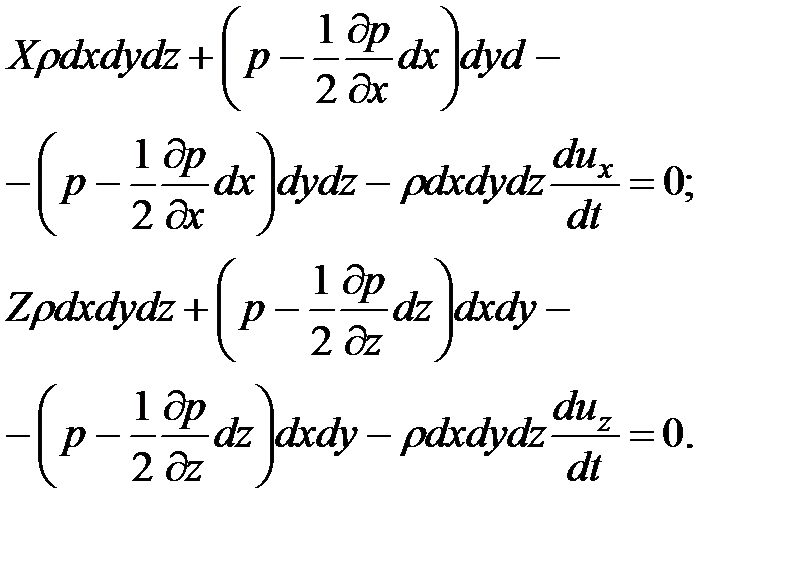
Раскрыв скобки и разделив полученные выше уравнения на 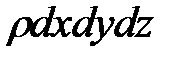, напишем

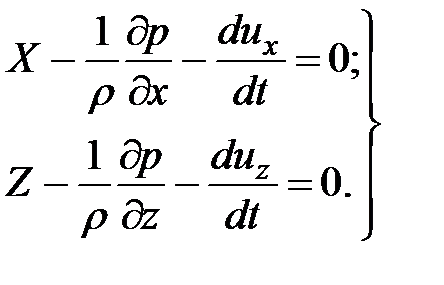(3.59)

Аналогично можно получить уравнение по оси у:

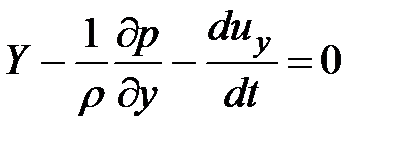(3.60)

Уравнения (3.59) и (3.60) можно записать в виде системы уравнений:

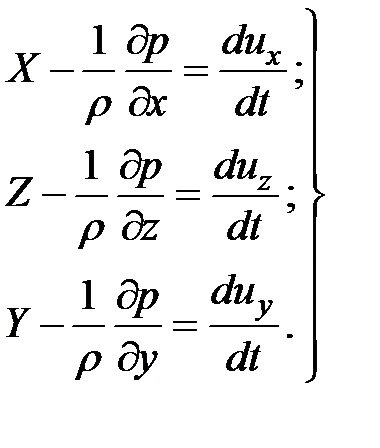(3.61)

В общем случае величины 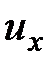, , 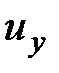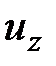являются функцией координат 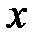, , 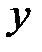, 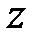а также времени 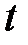. Следовательно, полный дифференциал скорости 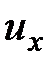будет

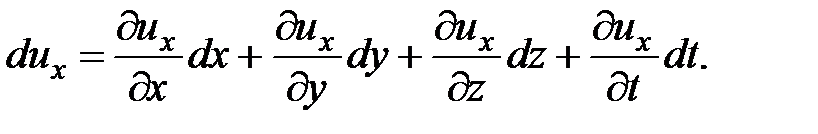(3.62)

Ускорение ;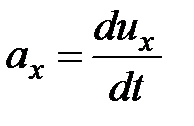

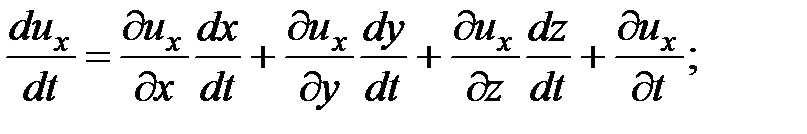
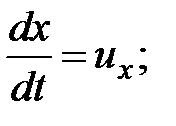
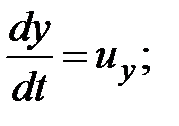
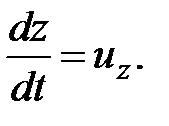
Тогда

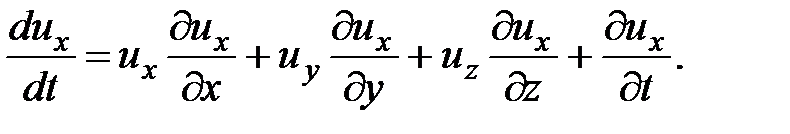(3.64)

Аналогично можно получить дифференциалы скоростей , .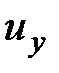

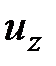После внесения в систему уравнений (3.61) дифференциалов скоросте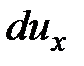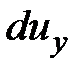й , и 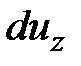она примет вид

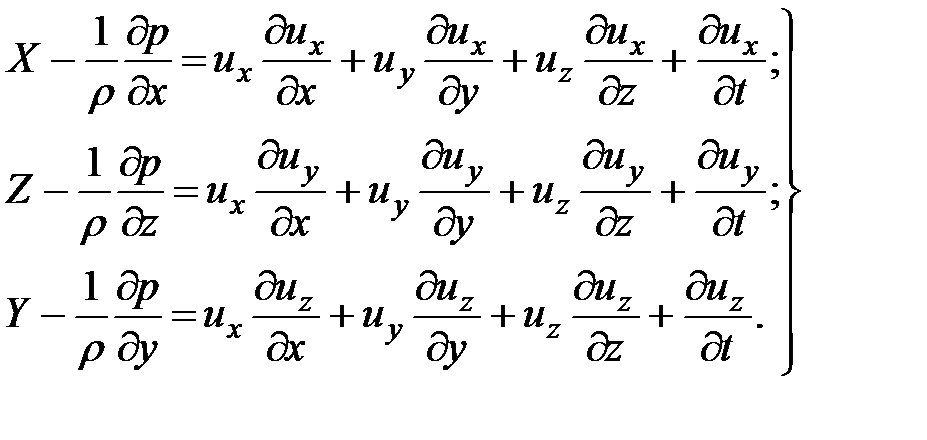(3.65)

В случае установившегося движения

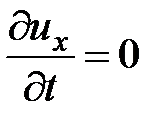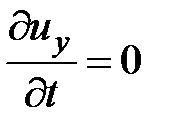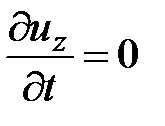; ; . (3.66)

Уравнения (3.65) представляют собой дифференциальные уравнения движения идеальной (невязкой) жидкости - уравнения Эйлера. Эти уравнения были получены Эйлером в 1775 г.

Уравнения Эйлера выражают связь между проекциями действующих сил, скоростей, давления и плотности жидкости. Уравнения Эйлера очень важны при изучении движения жидкости.

Для жидкости, находящейся в покое, имеем

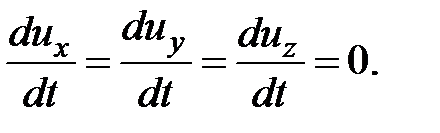
Дифференциальные уравнения Эйлера приобретают следующий вид:

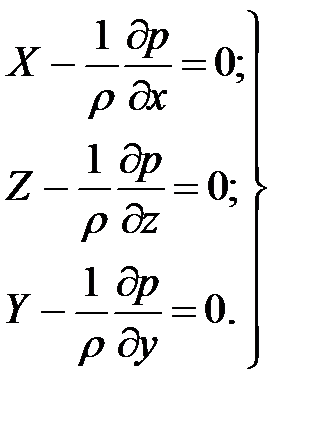(3.67)

Система дифференциальных уравнений является уравнениями равновесия жидкости.

Из уравнения равновесия можно получить основное уравнение гидростатики (2.2) (см. приложение).