Интегрирование уравнения движения Эйлера. Интеграл Бернулли
Рассмотрим установившееся движение идеальной жидкости. Уравнения Эйлера представим в виде (3.61). Умножим первое из уравнений на 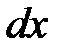 , второе - на
, второе - на 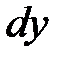 и третье - на
и третье - на  , получим
, получим
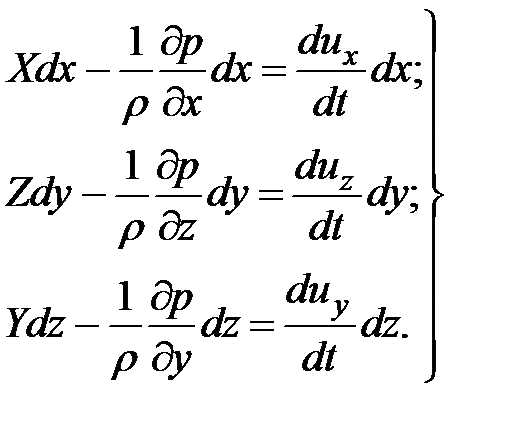 (3.68)
(3.68)
Сложим почленно все три уравнения системы:
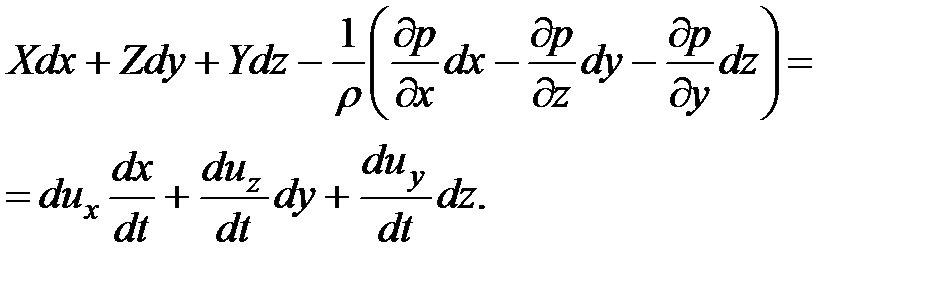 (3.69)
(3.69)
Для установившегося движения давление 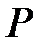 в точке является функцией ее координат и не зависит от времени. Поэтому дифференциал давления выражается в частных производных:
в точке является функцией ее координат и не зависит от времени. Поэтому дифференциал давления выражается в частных производных:
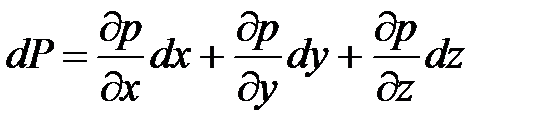 .
.
Так как 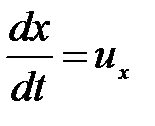 ;
; 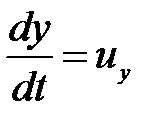 и
и 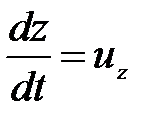 , то последний член уравнения (3.69)
, то последний член уравнения (3.69)
 , (3.70)
, (3.70)
кроме того
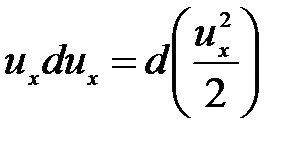 ;
; 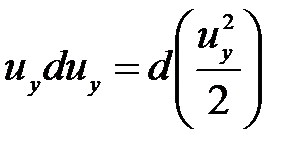 ;
; 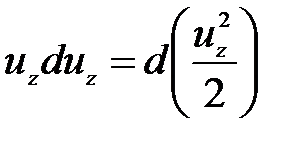 .
.
Следовательно, правая часть уравнения (3.69) примет вид
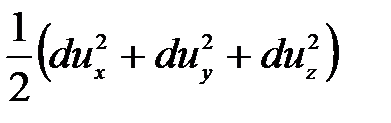 . (3.71)
. (3.71)
Полная (абсолютная) скорость и выражается через 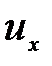 ,
,  ,
, 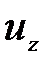 :
:
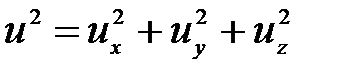 .
.
Тогда
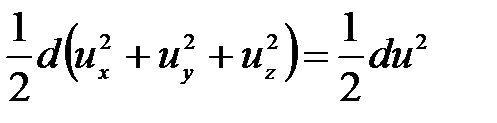 . (3.72)
. (3.72)
Уравнение (3.69) после преобразования можно переписать в следующем виде:
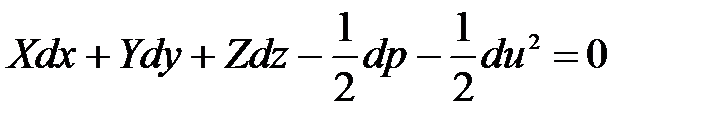 . (3.73)
. (3.73)
Первые три выражения в этом уравнении является полным дифференциалом силовой (потенциальной) функции 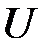 :
:
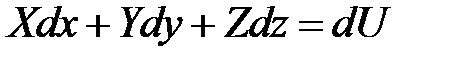 . (3.74)
. (3.74)
Таким образом, уравнение (3.74) примет вид
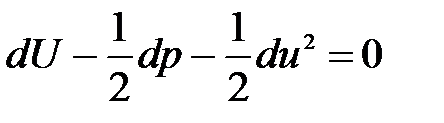 . (3.75)
. (3.75)
Проинтегрировав уравнение (3.75), получим
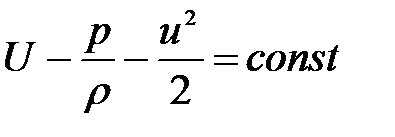 . (3.76)
. (3.76)
Данное выражение называют интегралом Бернулли-Эйлера.
Полученный трехчлен - уравнения сохраняет неизменное значение вдоль линии тока.
В случае когда движение происходит под действием только одной массовой силы - силы тяжести, то единичные массовые силы 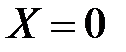 ,
,  ,
, 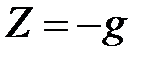 (ось
(ось 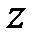 направлена вертикально вверх). Дифференциал силовой функции
направлена вертикально вверх). Дифференциал силовой функции
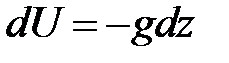 . (3.77)
. (3.77)
Уравнение (3.75) можно написать в следующем виде:
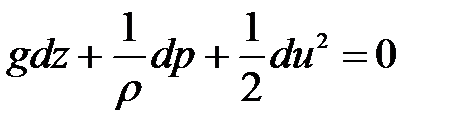 . (3.78)
. (3.78)
Разделим все слагаемые уравнения на ускорение свободного падения 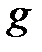 , тогда получим
, тогда получим
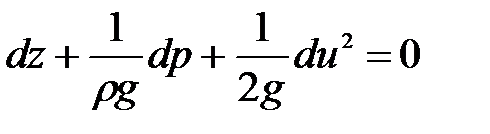 . (3 79)
. (3 79)
Приращение суммы всех трех членов этого уравнения при перемещении вдоль линии тока равно нулю.
Проинтегрировав дифференциальное уравнение (3.79), получим
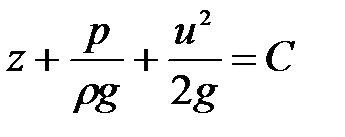 . (3.80)
. (3.80)
Сумма всех членов вдоль линии тока жидкости - величина постоянная, а следовательно, и вдоль идеальной элементарной струйки она также постоянна.
Уравнение (3.80), полученное с помощью уравнения движения Эйлера, для установившегося движения является уравнением Бернулли. Идентичное уравнение было получено ранее иным путем с использованием теоремы кинетической энергии (3.43).
Уравнение (3.80), записанное для двух живых сечений струйки, приобретает известный ранее вид
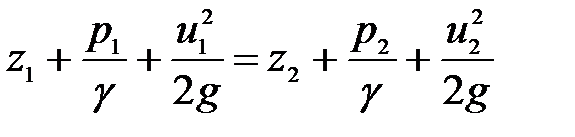 .
.
Дата добавления: 2015-12-29; просмотров: 919;
