ПОТОК ЖИДКОСТИ И ЕГО ПАРАМЕТРЫ

Согласно струйчатой модели поток жидкости - совокупность элементарных струек. Сечение потока 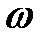, ограниченного конечными поверхностями, равно сумме живых сечений струек 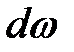. Это сечение называется живым сечением потока жидкости. Живое сечение должно быть нормальным к векторам скорости струи 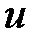, т.е. нормально к линиям тока:

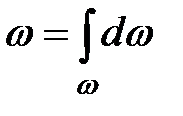. (3.15)

Общий объемный расход жидкости для потока жидкости в целом будет представлять собой сумму элементарных расходов струек:

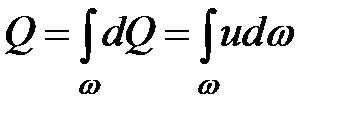. (3.16)

Расход жидкости можно представить в виде объемной фигуры, ограниченной, например, параболой, основание которой будет площадь живого сечения 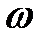(рис. 3.4).

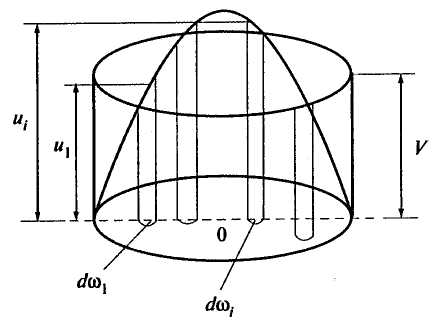
Рис. 3.4. К определению средней скорости

Объем этой фигуры .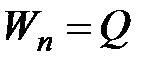

Чтобы определить расход, необходимо иметь аналитическую зависимость значения скорости 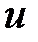от конечного положения элементарной площади струйки 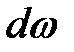. Скорость струйки является функцией координат 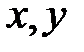: 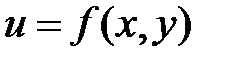. В связи с этим представляется весьма сложным произвести интегрирование уравнения расхода (3.16).

Для упрощения определения расхода потока жидкости вводится понятие о средней скорости. Принимается условие, что скорости струек по всему живому сечению потока постоянны, 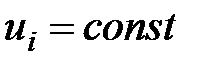. Таким образом, все частицы жидкости, проходящие через площадь 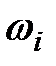, имеют одинаковую скорость .

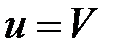Объему фигуры, ограниченной параболой вращения, соответствует объем цилиндра, высота которого равна средней скорости:

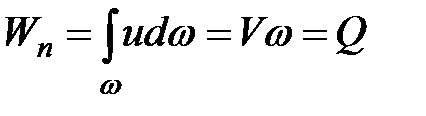(3.17)

Если живое сечение струек будет нормальным к вектору скорости 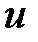в сечении потока жидкости, тогда элементарные струйки (линии тока) представляются в виде системы прямых параллельных друг другу линий, а живые сечения являются плоскими.

Движение жидкости, при котором имеет место некоторое расхождение линии тока (струек), что характеризуется малым углом и незначительной кривизной, называется плавно изменяющимся движением.

В случае плавно изменяющегося движения можно считать живые сечения плоскими, нормальными к вектору скорости.

На рис. 3.5 показано живое сечение цилиндрической трубы, по которому движется поток воды со средней скоростью 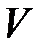, вектор которой нормален к поперечному сечению.

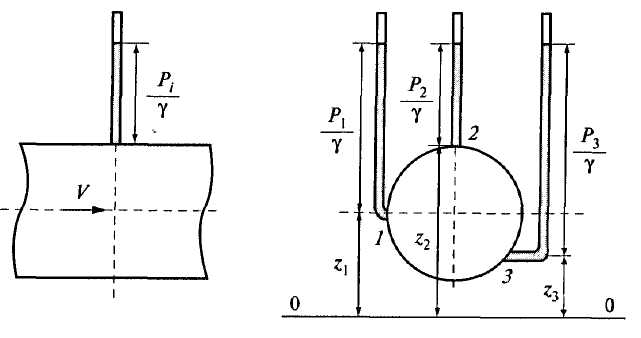
Рис. 3.5. Гидростатический напор в плоскости живого сечения

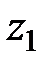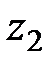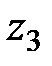К точкам 1, 2, 3 поперечного сечения трубы присоединены пьезометры. Положение точек относительно плоскости сравнения 0-0 - , , и . Пьезометрические высоты - , , 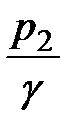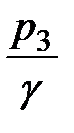имеют разные значения.

Сумма величин 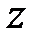и 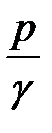, определяющих гидростатический напор, постоянна, т.е.

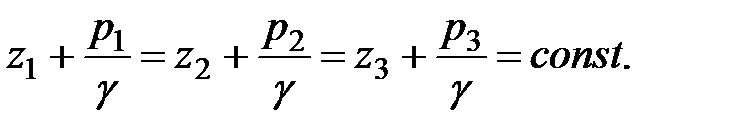
Таким образом, для любой точки живого сечения гидростатический напор 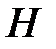относительно выбранной плоскости сравнения постоянен:

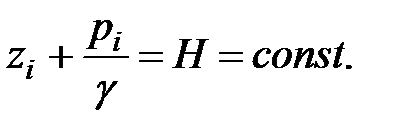
Установившееся движение, при котором поперечные сечения потока и средняя скорость в них одинаковы, называется равномерным движением. Примерами равномерного движения могут служить движения воды в трубе постоянного диаметра или в канале с постоянной глубиной и формой поперечного сечения.

Неравномерным называют установившееся движение, при котором поперечное сечение и средняя скорость изменяются по длине потока. Движение воды в трубе переменного диаметра является неравномерным.

Движение потока жидкости может быть напорным или безнапорным. При напорном движении поток ограничен твердыми поверхностями и жидкость полностью заполняет поперечные сечения по его длине. Поток жидкости не имеет свободной поверхности, и движение происходит за счет перепада напоров по длине.

Безнапорным движением называют движение, когда поток частично ограничен твердой поверхностью и имеет свободную поверхность. В большинстве случаев свободная поверхность граничит с атмосферой. Давление на свободную поверхность в этом случае будет равно атмосферному - 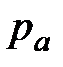. Примером может служить движение в трубах с не полностью заполненными поперечными сечениями или поток в канале, реке.