ПАРАМЕТРЫ СТРУЙКИ И ГИДРАВЛИЧЕСКОЕ УРАВНЕНИЕ НЕРАЗРЫВНОСТИ
Площадь поперечного элементарно малого сечения струйки жидкости называется живым сечением. Живое сечение нормально к линиям тока (рис. 3.2).
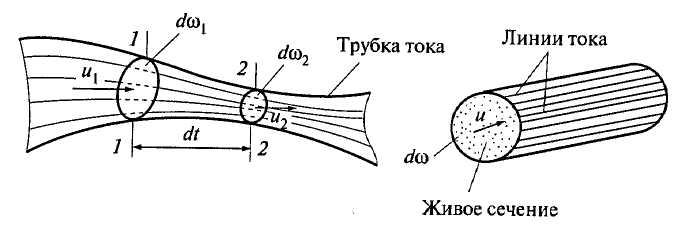
Рис. 3.2. Элементарная струйка
Скорость движения частиц в живом сечении - скорость струйки 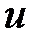 .
.
Расстояние вдоль струйки при известной скорости струйки 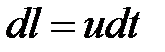 .
.
За определенное время 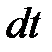 движущиеся частицы из сечения 1-1 переместятся в сечение 2-2, пройдя путь, равный
движущиеся частицы из сечения 1-1 переместятся в сечение 2-2, пройдя путь, равный 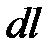 .
.
Таким образом, за время 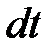 через первое живое сечение площадью
через первое живое сечение площадью 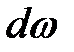 пройдет количество жидкости, равное объему элементарного цилиндра:
пройдет количество жидкости, равное объему элементарного цилиндра:
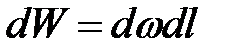 .
.
Объем жидкости, отнесенный к единице времени 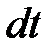 , - объемный расход (элементарный расход), который определяется по формуле, м3/с,
, - объемный расход (элементарный расход), который определяется по формуле, м3/с,
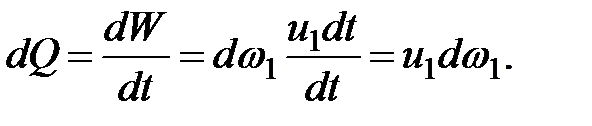 (3.9)
(3.9)
Количество жидкости, проходящей через живое сечение, можно представить через массу и вес жидкости.
Массовый расход струйки, кг/с,
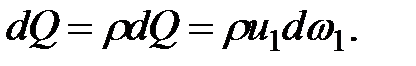 (3.10)
(3.10)
Весовой расход струйки, Н/с,
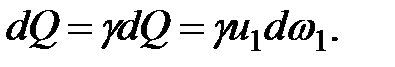 (3.11)
(3.11)
Расходом жидкости называется количество жидкости, проходящей через живое сечение за единицу времени.
Рассмотрим элементарную струйку несжимаемой жидкости при установившемся движении (рис. 3.3). Выделим в элементарной струйке объем между двумя сечениями 1-1 и 2-2 в некоторый момент времени. Используем свойства элементарной струйки и закон сохранения вещества (массы).
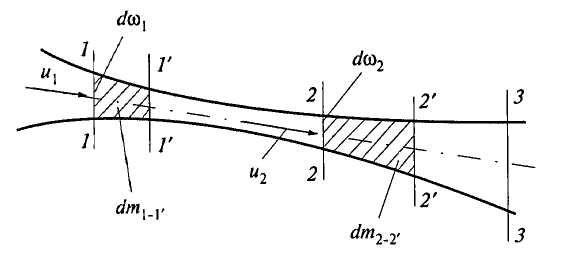
Рис. 3.3. К выводу уравнения неразрывности
За время 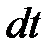 масса жидкости
масса жидкости 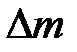 , находящаяся между сечениями 1-1 и 2-2, переместится в положение 1'-1' и 2'-2'.
, находящаяся между сечениями 1-1 и 2-2, переместится в положение 1'-1' и 2'-2'.
Массы жидкости между сечениями
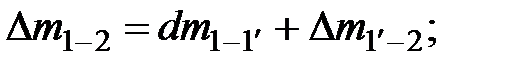
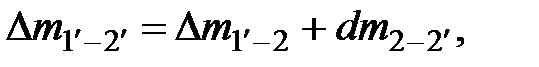
где 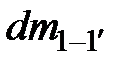 и
и 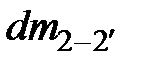 - элементарные массы жидкости, проходящие через сечения 1-1 и 2-2.
- элементарные массы жидкости, проходящие через сечения 1-1 и 2-2.
Масса жидкости остается неизменной при ее перемещении:
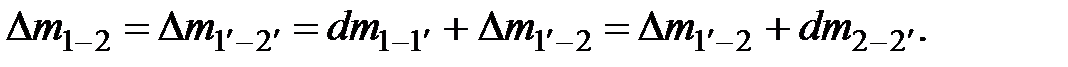
Следовательно, 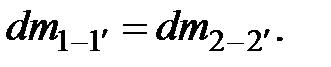 Масса жидкости, проходящая через любое сечение, равна
Масса жидкости, проходящая через любое сечение, равна
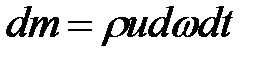 .
.
Масса жидкости, проходящая через первое и второе сечения струйки за время 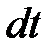 , составляет
, составляет
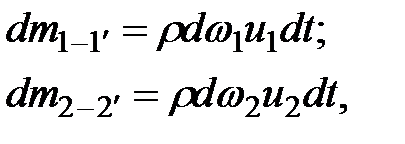
где 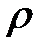 - плотность жидкости, находящейся в трубке тока.
- плотность жидкости, находящейся в трубке тока.
Таким образом,
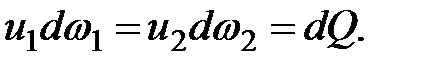 (3.12)
(3.12)
Аналогично можно получить соотношение скоростей и элементарных площадей для других сечений струйки.
Например,
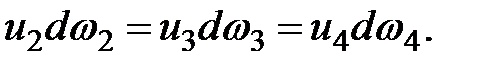
Таким образом, для любого сечения струйки 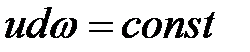 .
.
Уравнение неразрывности для элементарной струйки при установившемся движении утверждает, что элементарный расход во всех сечениях струйки постоянен.
Уравнение неразрывности записывается в следующем виде:
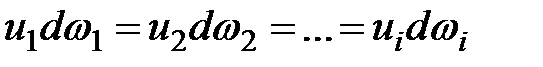 (3.13)
(3.13)
Скорости движения в разных сечениях струйки согласно (3.13) обратно пропорциональны элементарным площадям живых сечений струйки:
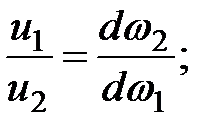
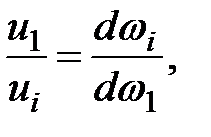 (3.14)
(3.14)
где 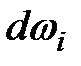 - произвольное живое сечение струйки, скорость струйки в нем
- произвольное живое сечение струйки, скорость струйки в нем 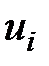 .
.
Дата добавления: 2015-12-29; просмотров: 602;
