ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ ТЕКУЧЕГО ТЕЛА (УРАВНЕНИЯ ЭЙЛЕРА)

Пусть 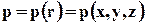- давление в жидкости. Выделим внутри жидкости куб с бесконечно малыми рёбрами dx, dy, dz и рассмотрим его равновесие под действием объёмных и поверхностных сил (рис.2.2).

Приравняем к нулю сумму проекций на ось х всех сил, действующих на куб.

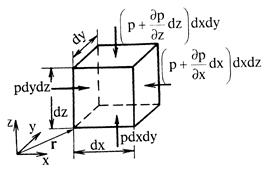Рис. 2.2. К выводу дифференциальных уравнений равновесия текучего тела

Плотность распределения массовой (объёмной) силы обозначим 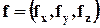, тогда объёмная сила, действующая на куб, будет иметь проекцию на ось х, равную .

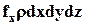Поверхностные силы на грани, нормальные осям y и z, дают нулевую проекцию на ось х, так как касательные напряжения в условиях гидростатики равны нулю. В пределах куба считаем, что в разложении р(х,у,z) в ряд Тейлора можно принять в расчёт лишь члены, линейно зависящие от приращения координат. Обозначим давление на левую грань куба, перпендикулярную оси х, через р(х,у,z), при этом на правой грани давление будет равно 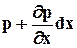. Если считать эти грани элементарными площадками в отношении давления, то проек­ция на ось х силы давления на левую грань равна р×dy×dz, а на правую равна 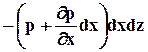. Сумма проекций всех поверхностных сил на ось х при этом окажется равной

.

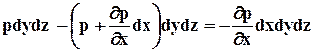Приравняв нулю сумму проекций поверхностных и объемных сил на ось х, имеем:

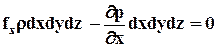. (2.2.1)

Разделив все слагаемые на р×dx×dy×dz, получим первое уравнение рав­новесия. Два других уравнения выведем аналогичным образом, проекти­руя силы на оси у и z. В результате получим систему дифференциальных уравнений равновесия (покоя) текучего тела (уравнений гидростатики Эй­лера):

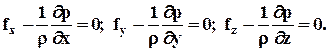(2.2.2)

Введём единичные векторы i, j и k, соответствующие координатным осям х, у и z:

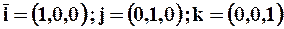. (2.2.3)

Умножим (2.2.2) на i, j и k, соответственно, и сложим их:

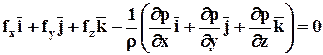
или в векторной форме

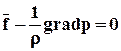. (2.2.4)

Векторное уравнение (2.2.4) равносильно системе трёх уравнений (2.2.3), где вектор grad p определяется через свои проекции на координатные оси в виде

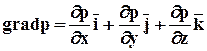(2.2.5)

либо в матричной форме

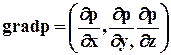. (2.2.6)