ПРЕДМЕТ И МЕТОД МЕХАНИКИ СПЛОШНОЙ СРЕДЫ

Механика сплошной среды - часть механики, изучающая движение газообразных, жидких и твёрдых деформируемых тел. В отличие от теоретической механики, здесь мы изучаем движение не отдельной материальной точки. В механике жидкости и газа считают, что материал, масса не сосредоточены в молекулах и атомах, а распределены, непрерывно рассредоточены в пространстве, занятом физическим телом. Такая гидромеханическая модель называется моделью сплошной среды. Это позволяет считать физические тела одинаковыми или различными в зависимости от интегральных характеристик (не учитывающих непосредственно детали молекулярной структуры тела). К таким характеристикам относят плотность, вязкость, теплопроводность среды, её скорость и т.п.

Поскольку сплошная среда не дискретна, то для определения указанных интегральных характеристик мы можем использовать предельные переходы. Например, плотность вещества (субстанции) в точке пространства с координатами определяется зависимостью

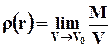, (1.1.1)

где V - объём, занятый веществом; М - масса этого объёма; V₀ - наименьший объём, окружающий точку с координатами , содержащий достаточно представительное число молекул.

Определим физический смысл объёма V_0. Пусть рассматриваемый нами объём V имеет форму куба. Пусть линейный размер куба равен 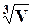. При 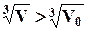плотность вещества мало изменяется в зависимости от 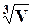, что связано с неоднородностью вещества, так как если вещество однородно, то r_ср от размеров V не зависит.

При 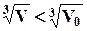изменение массы молекул, содержащихся в объёме V, реагирует на исключение из объёма отдельных молекул, т.е. использование модели сплошной среды становится сомнительным. Однако, учитывая малость размеров объёма V₀ ( 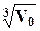~ 10^-7см), можно практически считать его равным 0. Т.е. для плотности можно записать

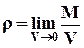, (1.1.2)

где V - бесконечно малая величина; r = r_сс; r_сс - плотность, определяемая в рамках модели сплошной среды. Аналогичные рассуждения можно использовать и при определении скорости движения жидкости или газа в рамках модели сплошной среды:

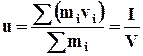. (1.1.3)

Использование предельных переходов, хотя и с определёнными допущениями, позволяет в случае применения модели сплошной среды эффективно применять аппарат дифференциального и интегрального исчисления.

Предметом изучения механики сплошной среды является изучение материальных тел, которые целиком заполняют пространство, причём расстояния между отдельными точками среды непрерывно меняются.

Непрерывным континуумом можно считать не только обычные материальные тела, но и различные поля, например, электромагнитное, гравитационное, поле излучения.

Движение - неотъемлемое свойство материи, поэтому в окружающем нас мире мы постоянно сталкиваемся с различными видами движения, многими из которых мы научились управлять и даже использовать, руководствуясь жизненным опытом и здравым смыслом.

Наряду с этим существуют виды движений, с которыми невозможно справиться, имея в запасе только здравый смысл и личный опыт. Существование таких движений вызвало необходимость развития механики сплошной среды как науки.

В нефтегазовом деле приходится сталкиваться с движением жидкостей и газа по трубам и внутри различных машин и механизмов. В этих условиях немаловажно знать законы взаимодействия жидкости с границами потока (особенно величины сопротивления подвижных и неподвижных твёрдых стенок), неравномерности распределения скоростных потоков, фильтрацию жидкостей и газов через пористую среду, равновесие жидкостей и тел, плавающих на поверхности жидкости, распространение волн и вибраций в твёрдых и жидких телах. Подавляющее число движений жидкостей и газов в каналах и трубопроводах имеет турбулентный характер, поэтому так важно экспериментальное и теоретическое изучение теории турбулентных потоков.

Изучаемая механикой сплошной среды теория упругости - основа создания машин и механизмов, без которых не может существовать развитое производство.

Помимо сказанного можно упомянуть о проблемах, связанных с движением всякого рода смесей: песков, грунтов, снега, сплавов и жидких растворов, суспензий и эмульсий, жидкостей с полимерными добавками и т.п.

Прежде чем приступить к решению прикладных задач механики сплошной среды, необходимо освоить теоретический курс, в котором рассматриваются математические методы изучения движения деформируемых тел. Для этого вводится ряд понятий, которые характеризуют и однозначно определяют движение сплошной среды. Среди таких понятий можно назвать поле скоростей, температуру, циркуляцию скорости и т.д.

Механика сплошной среды разработала методы сведения механических задач к математическим, то есть в конечном итоге мы должны отыскать либо численные значения искомых величин, либо числовые функции с помощью различных математических операций. Помимо решения конкретных задач механика сплошной среды занимается установлением общих свойств и законов движения деформируемых тел. Например, установлением связи между давлением и скоростью, между внешними нагрузками и возникающими в результате деформациями.

Гипотеза сплошности. Введение идеального понятия сплошной среды необходимо потому, что при исследовании движения деформируемых тел мы хотим пользоваться математическим аппаратом непрерывных функций, дифференциальным и интегральным исчислением.

Радиус атомного ядра равен приблизительно 10^-13см, радиус молекулы водорода - 10^-8см, то есть, радиус атомного ядра намного меньше радиуса молекулы, несмотря на то, что именно в нём сосредоточена основная масса вещества (масса протона имеет порядок 10^-24г, электрона - 10^-28г). С другой стороны, при н.у. в 1 кубическом миллиметре воздуха находится 27 × 10⁹ частиц!

В межзвёздной среде находится сильно разреженный газ, но для космоса характерны такие расстояния, при которых даже такую концентрацию газовых частиц можно рассматривать как сплошную среду.

Например, у железа отношение плотности материала к плотности ядерного вещества составляет 7 × 10^-14 , то есть, объёмы, занимаемые телами, намного больше объёмов, в которых сосредоточено собственно вещество. Итак, большинство тел состоит из «пустоты», хотя в то же время в практически малых объёмах пространства, занятого телами, всегда сосредоточено большое количество частиц.

Между частицами вещества имеются взаимодействия, причём взаимодействия более сильные в жидкостях и твёрдых телах, где частицы расположены ближе друг к другу. Силы, обеспечивающие упругость тел и их прочность, имеют электрическую природу и сводятся к силам Кулона и взаимодействиям элементарных магнитов. Зная электрические силы взаимодействия между частицами, можно строить теорию твёрдых деформируемых тел.

При изучении движения сплошной среды необходимо вводить внутренние напряжения. В телах с дискретным молекулярным строением внутренние напряжения являются статистически средними, обусловленными силами взаимодействия между молекулами, расположенными по разные стороны от рассматриваемого сечения, а также переносом макроскопического количества движения через это сечение, в результате теплового движения молекул.

Свойство вязкости в газах объясняется действием теплового движения молекул, которое выравнивает макроскопические движения соседних частиц газа. Таким образом, свойства внутренних напряжений в материальных средах определяются их молекулярным составом, силами взаимодействия между молекулами и атомами (которые проявляются только на очень близких расстояниях) и тепловым движением, которое характеризуется температурой.

В принципе, установление макроскопических законов на основании глубокого анализа физических микроскопических механизмов и свойств элементарных частиц составляет одну из главных задач физики.

С точки зрения физики казалось бы целесообразным развивать механику на базе представления о материальном теле как совокупности элементарных частиц. Следить за движением каждой элементарной частицы из-за их весьма большого числа практически невозможно. Тем более, что для практики не требуется знать движение каждой элементарной частицы, а достаточно каких-то средних, суммарных характеристик. Поэтому одним из методов исследования материальных сред является статистический.

Другим методом является построение феноменологической макроскопической теории на основе опытных закономерностей и гипотез. Это очень эффективный путь, тем более что в этом случае решённые задачи могут быть проверены на опыте.

Пространство и время.В природе нам не даны ни неподвижное пространство, ни его метрика; нам не дано и равномерное движение, по которому можно было бы отсчитывать равные промежутки времени.

В пределах приемлемых приближений, в классической механике пространство, по отношению к которому рассматривают движение механических систем, считают неподвижным и принимают евклидовым.

За единицу абсолютного времени принимаются средние солнечные сутки. Под пространством понимают совокупность точек, задаваемых с помощью чисел, называемых координатами. Непрерывное метрическое многообразие - это пространство, в котором определены расстояния между точками. В трёхмерном евклидовом пространстве с декартовой системой координат расстояние между двумя любыми точками определяется формулой:

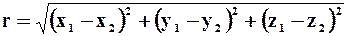. (1.1.4)

Рис.1.1. Системы координат

В дальнейшем мы будем рассматривать только такие пространства, в каждом из которых можно ввести единую для всех точек декартову систему координат. Такие пространства называют евклидовыми.

Время может зависеть от системы отсчёта наблюдателя. Время, которое течёт одинаково для всех наблюдателей, называется абсолютным. Это тоже идеализация.

Таким образом, обобщая сказанное, можно сформулировать следующие основные гипотезы механики сплошной среды:

Ø среда - континуум, в котором материя распределена сплошным образом;

Ø рассматриваем движение среды только в евклидовом пространстве;

Ø движение осуществляется в течение абсолютного времени.

Механика сплошной среды возникла в связи с решением таких задач, как установление закономерностей истечения жидкостей из сосудов, просачивание жидкости через грунт и т.п.

В настоящее время механику сплошной среды делят на 2 крупные области: гидромеханику (механику жидкости и газа) и механику твёрдых деформируемых тел.

Гидромеханика включает в себя:

· механику идеальной жидкости;

· механику вязкой ньютоновской жидкости;

· механику аномально вязкой неньютоновской жидкости;

· механику турбулентных течений.

Механика деформируемых твёрдых тел изучает:

· теорию упругости;

· теорию пластичности;

· теорию ползучести;

· теорию разрушения;

· механику сыпучих тел.

1.2. ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ГИДРОМЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК В СПЛОШНОЙ СРЕДЕ

Плотность распределения той или иной гидромеханической характеристики в пространстве или на поверхности это количество этой характеристики, приходящееся на единицу объёма или площади поверхности. Иначе говоря, это функция координат и времени 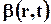, которая, будучи умножена на элементарный объём DV (или элементарную площадку DА), отразит количественно рассматриваемую гидромеханическую характеристику этого объёма (площадки). Пусть кинетическая энергия элементарного объёма DV, имеющего массу 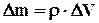и скорость 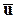, равна

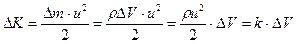. (1.2.1)

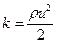- плотность распределения кинетической энергии.

Если рассматриваемая величина - вектор, то эта функция может быть вектором. Например, количество движения этого же элементарного объёма DV равно

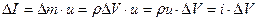, (1.2.2)

где 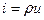- плотность распределения количества движения.

Пусть В(t) - общее количество какой-либо гидромеханической характеристики объёма V в момент времени t, а 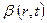- плотность распределения этой характеристики. Разделим объём V на элементарные объёмы 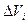, где i - порядковый номер элементарного объёма. Количество рассматриваемой гидромеханической характеристики в пределах i -го элементарного объёма равно 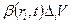, где 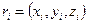- координаты любой внутренней точки объёма 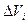. Подсчитаем общее количество характеристики, относящееся к объёму V:

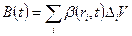. (1.2.3)

Рассматривая элементарный объём как бесконечно малую величину, можно записать

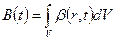. (1.2.4)

Исходя из сказанного плотность жидкости 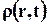можно назвать плотностью распределения массы (в пространстве), при этом массу М объёма V можно представить в виде

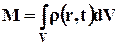. (1.2.5)

В зависимости от того, к какой гидромеханической характеристике относится функция плотности распределения 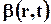, она может быть как скалярной, так и векторной.