Интерполяционная формула Лагранжа.

При построении интерполяционной формулы Лагранжа в качестве 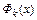используются полиномы Лагранжа степени n, удовлетворяющие условиям

Для выполнения второго условия полином степени n должен иметь вид

,

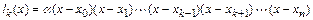т. е. его корнями являются все узлы интерполяции, кроме k-го. Коэффициент 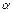определим, используя первое условие:

.

Отсюда находим

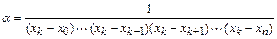
и

.

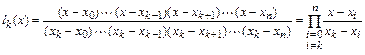Решение системы (7.3) при использовании в качестве элементарных функций полиномов Лагранжа имеет вид 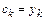. Таким образом, интерполяционный многочлен Лагранжа представится как

.

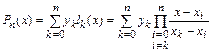Преобразуем его к виду, используемому на практике при вычислении значений функции:

.

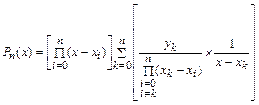Интерполяционный многочлен совпадает с интерполируемой функцией только в точках . В остальных точках имеет место погрешность интерполяции

,

которая оценивается величиной

,

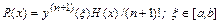где 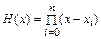. (Вывод оценки погрешности опустим). Погрешность интерполяции зависит от числа узлов интерполяции n, а также от их расположения на отрезке 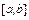. Наилучшими узлами интерполяции следует признать те 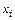, для которых принимает наименьшее значение.

Недостатком интерполяционной формулы Лагранжа является то, что каждое слагаемое зависит от всех узлов интерполяции. При добавлении узла интерполяции и, следовательно, повышении порядка полинома необходимо вычислять не только слагаемое, относящееся к новому узлу, но и перевычислять заново слагаемые, относящиеся ко всем узлам интерполяции.