Понятие конечных и разделенных разностей.
Пусть на равномерной сетке в узлах  заданы значения функции
заданы значения функции 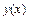 , т. е.
, т. е.
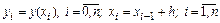 .
.
Конечными разностями первого порядка называют величины
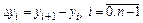 .
.
Разности конечных разностей первого порядка называют конечными разностями второго порядка:
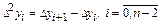 .
.
Аналогично определяют конечные разности следующих порядков:
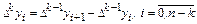 .
.
Схему вычисления конечных разностей удобно представить в виде следующего треугольника:
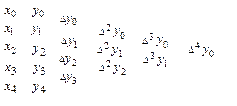
Если узлы интерполяции – произвольные точки, то вводится понятие разделенных разностей.
Разделенная разность первого порядка:
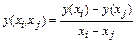 .
.
Разделенная разность второго порядка:
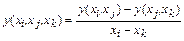 .
.
Разделенная разность k-го порядка:
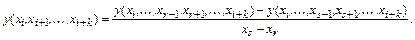 Отметим два важных свойства разделенных разностей:
Отметим два важных свойства разделенных разностей:
1. Разделенная разность является симметричной функцией своих аргументов, т. е. значение разделенной разности не зависит от порядка перечисления узлов интерполяции, а зависит только от их значений;
2. Разделенная разность вычисляется и тогда, когда две или более точки интерполяции одинаковы.
Разделенная разность первого порядка в случае, когда одинаковы две точки, имеет вид
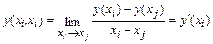 .
.
Если точка 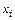 среди узлов интерполяции встречается (m+1) раз, то разделенная разность m-го порядка на этих узлах
среди узлов интерполяции встречается (m+1) раз, то разделенная разность m-го порядка на этих узлах
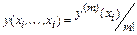 .
.
Приведем теперь схему вычисления разделенных разностей
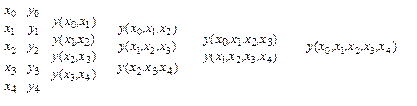
Дата добавления: 2015-11-24; просмотров: 1147;
