Интерполяционная формула Ньютона.

Пусть 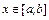. Построим первую разделенную разность

.

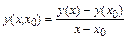Откуда находим

.

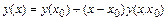Построим вторую разделенную разность

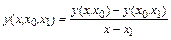
и выразим из нее :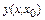

.

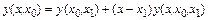Подставим 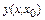в выражение для :

.

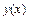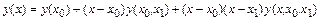Аналогично привлекаем следующие узлы интерполяции для построения интерполяционной функции.

После использования всех узлов интерполяции:

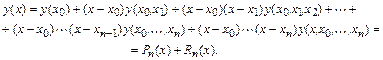Таким образом, интерполяционный многочлен Ньютона имеет вид

.

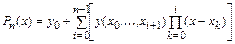Непосредственной проверкой нетрудно убедиться, что

.

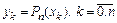Погрешность интерполяции

.

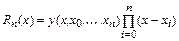Более эффективное вычисление значения функции по интерполяционной формуле Ньютона можно получить, если преобразовать ее к такому виду:

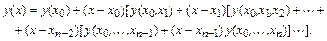
Интерполяционная формула Ньютона позволяет легко наращивать число узлов интерполяции, требуя при этом вычисления лишь дополнительных слагаемых. Например, добавление узла 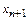приведет к вычислению слагаемого

.

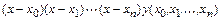Лекция 8

Сплайн-интерполяция

ЦЕЛЬ ЛЕКЦИИ: Показать ограничения полиномиальной интерполяции, ввести понятие m-сплайна, построить вычислительную схему интерполяции на основе кубического сплайна.