Дискретный метод Ньютона.

Дискретный метод Ньютона базируется на аппроксимации матрицы Якоби на основе вычисленных значений функции 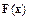в ряде вспомогательных точек. Построим его. Как и прежде, будем использовать векторную запись решаемой системы уравнений

.

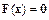Пусть известно k-е приближение 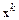к решению 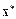. Аппроксимируем функцию 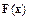линейной функцией:

.

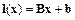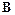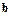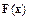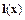Для численного определения матрицы и вектора потребуем, чтобы значения функций и совпадали в (n+1) вспомогательных точках 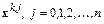, т. е. чтобы выполнялось равенство

.

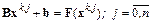Вычитая из первого равенства все последующие, получим соотношения

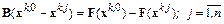
или в матричной форме

,

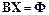где 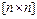матрицы 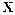и 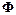имеют вид

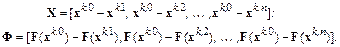
Следовательно,

.

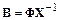Условие 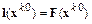позволяет найти вектор :

.

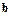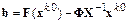Перепишем функцию 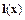, подставив найденные соотношения для 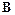и :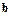

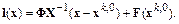
Примем 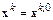. Будем искать 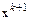из уравнения

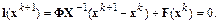
Получим итерационную формулу дискретного метода Ньютона:

.

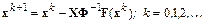Заменяя обращение матрицы решением линейной системы, придем к реализуемому на практике алгоритму дискретного метода Ньютона:

1. Вычисляется вектор 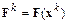, матрицы 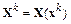и .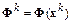

2. Решается система линейных алгебраических уравнений

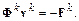
3. Вычисляется вектор поправки

.

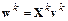4. Вычисляется (k+1)-е приближение

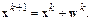
5. Пункты 1÷4 повторяются для k=0,1,2,… до получения решения с требуемой точностью.

Применение дискретного метода Ньютона предполагает хранение 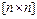-матриц 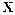и 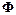. Однако на практике в качестве вектора 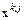выбирается вектор

,

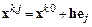где 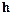– диагональная матрица параметров дискретизации, 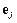– j-й столбец единичной матрицы. Элементы 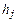матрицы 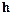вычисляют по правилу 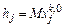, где 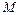– константа (например, 0.1).