Метод Ньютона для решения систем нелинейных уравнений.
Пусть задана система нелинейных уравнений
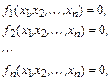
решение которой достигается в точке 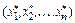 пространства
пространства 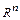 . Обозначим
. Обозначим 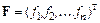 ;
; 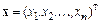 . Тогда исходная система запишется в виде
. Тогда исходная система запишется в виде
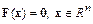 .
.
Предположим, что известно k-е приближение  к
к 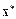 . Построим правило Ньютона вычисления (k+1)-го приближения в форме
. Построим правило Ньютона вычисления (k+1)-го приближения в форме
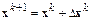 .
.
Разложим функцию 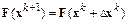 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 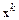 и сохраним в разложении два члена:
и сохраним в разложении два члена:
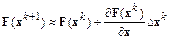 .
.
Полагая, что решение системы достигается на текущей итерации, относительно поправки 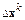 получим систему линейных алгебраических уравнений:
получим систему линейных алгебраических уравнений:
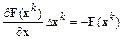 .
.
Тогда
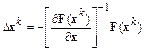 ,
,
и итерационное правило Ньютона решения системы нелинейных алгебраических уравнений запишется как
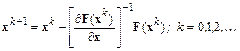
Такой вид метода Ньютона неудобен на практике, потому что требует вычисления обратной матрицы, а эта операция достаточно трудоемка. На практике метод Ньютона реализуется в следующем виде:
1. Решается система линейных алгебраических уравнений и вычисляется вектор поправки:
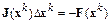 ,
,
где 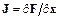 – матрица Якоби системы;
– матрица Якоби системы;
2. Вычисляется (k+1)-е приближение
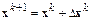 ,
,
3. Пункты 1, 2 повторяются для k=0,1,2,… до тех пор, пока не будет достигнута требуемая точность.
Критерием завершения итерационного процесса служат условия
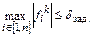 ,
, 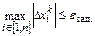 ,
,
или в более общей форме
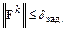 ,
, 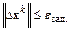 .
.
Дата добавления: 2015-11-24; просмотров: 879;
