ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ. МЕТОД ИТЕРАЦИй.

ЦЕЛЬ ЛЕКЦИИ: Для уравнения 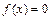ввести постановки задач отделения и уточнения корней, сформулировать лемму об оценке погрешности приближенного решения, построить метод простой итерации, получить для него оценку точности, доказать его сходимость.

Пусть требуется решить уравнение

,

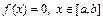т. е. найти все корни , удовлетворяющие этому уравнению на отрезке .

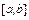Задача численного решения уравнения сводится, во-первых, к отделению корней, во-вторых, к последующему уточнению корней.

Отделение корней.

Отделить корни уравнения 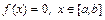значит заключить каждый корень в интервал

,

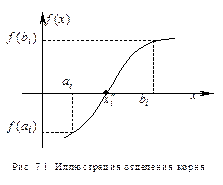
для которого выполняются условия:

1. ;

2. 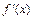– знакопостоянная функция для .

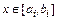Первое неравенство обеспечивает наличие в интервале 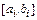хотя бы одного корня, второе условие гарантирует единственность корня (см. рис. 4.1).

Для отделения корней можно использовать аналитический и табличный способы.

Аналитический предполагает исследование функции 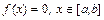методами математического анализа, последующее построение графика функции, из которого и определяются интервалы, содержащие единственный корень. Недостаток аналитического способа – неалгоритмизуемость.

Табличный метод предполагает составление таблицы значений 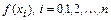, причем 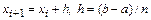. Из таблицы на основании условий

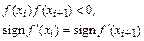
алгоритмически определяются искомые интервалы 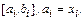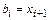. Чтобы не потерять корни, интервал отделения h должен быть достаточно малым.

Уточнение корней.

Пусть 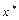- корень уравнения

.

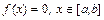В дальнейшем 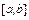– интервал, содержащий единственный корень.

Уточнить корень с заданной точностью значит найти приближенное значение такое, что

.

Для решения сформулированной задачи необходимо уметь производить оценку абсолютной погрешности метода, т. е. величины .