Лемма об оценке погрешности приближенного решения уравнения .

Лемма. Пусть уравнение 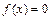на отрезке 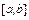имеет корень 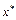. Пусть найдено некоторое его приближенное значение . Тогда

,

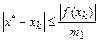где

.

Доказательство. Вычислим по теореме о конечных приращениях:

.

Очевидно, что

.

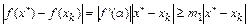Отсюда

,

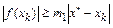или

.

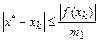Лемма доказана.

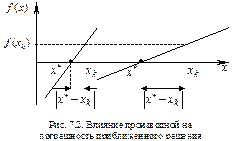
Величину 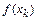называют невязкой. Из леммы следует, что судить о величине погрешности приближенного решения только по величине невязки нельзя. Необходимо учитывать и значение первой производной. Обратимся к рис. 4.2. Из этого рисунка следует, что одна и та же невязка приводит к существенно разным погрешностям приближенного решения, если производная в окрестности решения сильно отличается.

Метод итераций.

Для построения метода итераций преобразуем уравнение

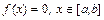
к виду

.

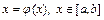Это можно сделать в общем случае так:

,

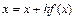или 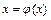, где

.

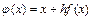Постоянный множитель h выбирается при этом из условия сходимости метода (установим его позже).

Пусть известно начальное приближение 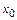. Тогда

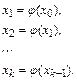
Приведенный способ построения числовой последовательности 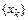реализуется в методе итераций:

.

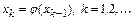Рассмотрим, как ведет себя погрешность решения на итерациях метода. Обозначим 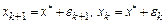, где 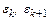- погрешности приближенного решения на двух соседних итерациях. Подставим представленные таким образом и 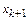в итерационное правило:

.

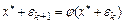Разложим функцию в ряд Тейлора в окрестности точки :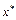

.

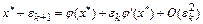Пренебрегая остаточным членом 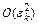, получим соотношение, связывающее погрешность решения метода на двух соседних итерациях:

.

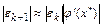Сделаем некоторые выводы на основании этого приближенного равенства.

· Если 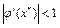, то можно ожидать, что 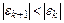и последовательность 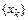будет сходиться к решению, когда начальное приближение 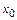выбрано достаточно близким к .

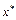· Если 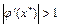, то скорее всего 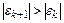и метод будет расходиться, так как каждое последующее приближение будет отстоять от

решения дальше, чем предыдущее.

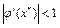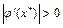· При и погрешност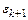и и 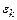имеют одинаковые знаки. Сходимость будет монотонной.

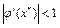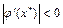· При и погрешност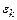и и 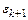имеют разные знаки. Сходимость является немонотонной.

Проиллюстрируем характер сходимости метода итераций графически. Образуем функции 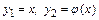. В решении задачи значения этих функций совпадают. Первый пример (см. рис. 7.3,а) соответствует условиям

и, следовательно, в этом случае наблюдается монотонная сходимость метода итераций. В следующем примере (см. рис. 4.3,б)

,

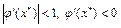поэтому имеет место немонотонная сходимость. В последнем примере (см. рис. 4.3,в)

.

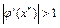При таких значениях производной метод итераций расходится.

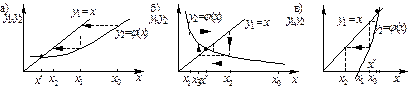
Рис. 4.3. Иллюстрация сходимости метода итераций