Методы продолжения по параметру.
Эти методы позволяют обеспечить сходимость метода Ньютона от выбранного начального приближения 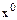 .Сущность методов продолжения по параметру заключается в замене исходной задачи последовательностью задач, каждая последующая задача при этом незначительно отличается от предыдущей. Последовательность строится таким образом, что первая система имеет решение
.Сущность методов продолжения по параметру заключается в замене исходной задачи последовательностью задач, каждая последующая задача при этом незначительно отличается от предыдущей. Последовательность строится таким образом, что первая система имеет решение 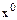 , а последняя система совпадает с исходной задачей. Поскольку системы отличаются незначительно, то решение предыдущей задачи окажется хорошим начальным приближением для последующей. Решая такую последовательность задач методом Ньютона, получим в итоге решение исходной системы. Рассмотрим способ построения указанной последовательности задач.
, а последняя система совпадает с исходной задачей. Поскольку системы отличаются незначительно, то решение предыдущей задачи окажется хорошим начальным приближением для последующей. Решая такую последовательность задач методом Ньютона, получим в итоге решение исходной системы. Рассмотрим способ построения указанной последовательности задач.
Пусть при решении системы
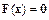
используется начальное приближение 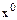 . Заменим исходное уравнение
. Заменим исходное уравнение 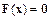 уравнением с параметром
уравнением с параметром
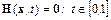 ,
,
которое при 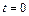 имеет решение
имеет решение 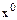 , а при
, а при 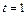 совпадает с решением исходной задачи, т. е.
совпадает с решением исходной задачи, т. е.
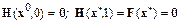 .
.
В качестве 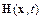 можно выбрать функции
можно выбрать функции
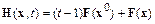
либо
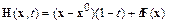 .
.
Разобьем отрезок 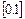 точками
точками 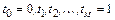 на
на 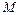 интервалов. Получим искомую последовательность систем:
интервалов. Получим искомую последовательность систем:
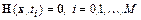 .
.
Дата добавления: 2015-11-24; просмотров: 1128;
