Схема итерационных методов.

Пусть требуется решить систему

.

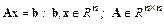Предположим, что Q – неособенная 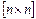-матрица, рассматриваемая как апроксимация матрицы A, для которой решение системы

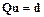
не представляет особого труда. Это имеет место тогда, когда матрица Q является нижней треугольной, верхней треугольной, трёх-диагональной, произведением конечного числа таких простых матриц и т.п. Матрицу Q называют матрицей расщепления.

Перепишем исходную систему в виде

.

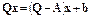Построим итерационный процесс

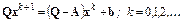
Разрешим его относительно :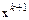

,

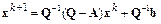или

.

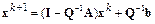Введем обозначения:

; .

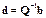Тогда итерационную схему можно представить в виде

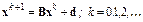
Это линейная схема первого порядка. Поскольку итерационная матрица B на итерациях является постоянной, то такую схему называют стационарной.

Достаточное условие сходимости этой итерационной схемы имеет вид

.

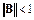Убедимся в этом.

Обозначим вектор погрешности на k-м шаге через 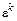, на (k+1)-ом шаге – 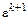, точное решение – . Тогда

.

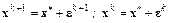Учет этих соотношений в итерационной схеме позволяет записать

Отсюда

.

При видно, что 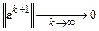, т. е. метод сходится к решению. Построим теперь вычислительные схемы, выбирая конкретный способ формирования матрицы раcщепления.