Устойчивость и точность метода LU-факторизации.

Метод LU-факторизации, если не делать никаких специальных усилий, характеризуется такими же оценками нормы матрицы возмущения и относительной ошибки, как и метод Гаусса. В то же время этот метод наряду с упоминавшимися при рассмотрении метода Гаусса направлениями повышения точности решения имеет еще одну возможность: использование так называемой операции скалярного накопления. Эта операция во многих ЭВМ реализована аппаратно либо моделируется специальными подпрограммами. Операция скалярного накопления привлекается при вычислении скалярного произведения

.

Пусть основным режимом работы ЭВМ является арифметика с плавающей точкой и t-разрядной мантиссой машинного слова. Рассмотрим вычисление скалярного произведения. Произведение чисел βk и γk, выполненное арифметическим процессором, имеет 2t–разрядную мантиссу. Вместо того, чтобы округлить это произведение до t разрядов и прибавить результат к хранимой t–разрядной промежуточной сумме Sk-1, режим накопления предусматривает удержание 2t разрядов как для Sk-1, так и для βkgk. Очередное суммирование 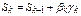выполняется с 2t-разрядными числами. Оно также сопровождается ошибкой округления, но эта ошибка затрагивает лишь последний разряд 2t–разрядного результата. Возвращение к t–разрядному представлению происходит лишь после вычисления скалярного произведения.

Анализ расчетных соотношений метода LU-факторизации свидетельствует о том, что они реализуются с использованием операции скалярного накопления.

Оценка нормы матрицы возмущений метода LU-факторизации при использовании операции скалярного накопления имеет вид

.

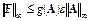Устойчивость вычислительной схемы метода определяется величиной коэффициента роста элементов матрицы A. Чтобы уменьшить величину g(A), в методе LU-факторизации используется столбцовая процедура выбора главных элементов.

Погрешность решения метода

.