Устойчивость алгебраических методов.

Прямые методы в отсутствии ошибок округления позволяют получить точное решение системы

.

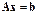Современные вычислительные машины оперируют с конечными десятичными дробями, представленными в форме с плавающей точкой. В этом случае уже на этапе запоминания элементов матрицы A и вектора 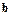в памяти ЭВМ вносится ошибка округления и реально решается возмущенная система

.

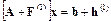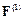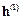Здесь и – возмущения матрицы системы и вектора правой части.

Для элементов 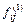матрицы 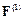и компонент 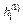вектора 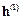справедливы оценки

,

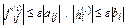где 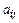– элемент матрицы A, 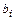– компонент вектора 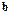, ε – число, характеризующее относительную погрешность машинной ариф-метики. Например, для двоичных ЭВМ, использующих арифметику с плавающей точкой и t – разрядную мантиссу, .

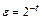Перейдем к более общей числовой оценке возмущений – норме. Из записанных выше неравенств следует, что

,

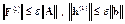где знаком 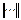обозначена какая-либо норма вектора и согласованная с ней норма матрицы.

Поясним теперь суть одного из наиболее разработанных подходов к анализу устойчивости алгебраических методов.

Пусть 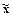– приближенное решение СЛАУ, полученное применением некоторого прямого метода. Очевидно, что вследствие ошибок округления при реализации на ЭВМ прямого метода это решение не будет точно удовлетворять системе 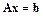. Пусть, однако, удается показать, что 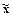является точным решением системы

.

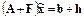Если для матрицы F и вектора 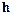, называемых эквивалентными возмущениями метода, можно получить оценки вида

,

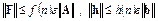где f(n), h(n) - некоторые степенные функции типа 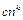с небольшим показателем k, то метод считается устойчивым по Уилкинсону. Такой вид функций f(n), h(n) объясняется тем, что в процессе реализации прямых методов на ЭВМ неизбежно некоторое накопление ошибок округления, пропорциональное числу арифметических операций, за которое прямой метод приводит к решению.