Точность алгебраических методов.
Рассмотрим влияние возмущений матрицы системы и вектора правой части на точность решения. Относительная погрешность решения
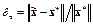 ,
,
где  – точное решение, в любой согласованной норме подчиняется неравенству
– точное решение, в любой согласованной норме подчиняется неравенству
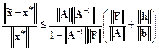 .
.
Обозначим
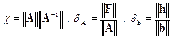 .
.
Величины 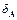 ,
, 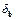 являются оценками относительных возмущений матрицы A и вектора b. Число χ есть не что иное, как число обусловленности матрицы A.
являются оценками относительных возмущений матрицы A и вектора b. Число χ есть не что иное, как число обусловленности матрицы A.
Естественно допустить, что
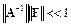 .
.
Такое неравенство означает, что норма матрицы возмущений существенно меньше нормы исходной матрицы, т. е. предполагается, что прямой метод решения линейной системы устойчив. В этом случае
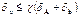 .
.
Относительная ошибка решения системы прямым методом может достигать величины, определяемой произведением числа обусловленности и суммы относительных возмущений матрицы системы и вектора правой части. Если число обусловленности велико, то даже при малых эквивалентных возмущениях матрицы и вектора правой части погрешность решения линейной системы оказывается значительной.
Задачи, для которых χ велико, называют плохо обусловленными. Число обусловленности зависит от выбора матричной нормы. Например, для симметричной положительно определенной матрицы A в качестве 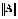 можно взять ее максимальное собственное число. Тогда число обусловленности
можно взять ее максимальное собственное число. Тогда число обусловленности
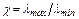 ,
,
где 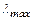 ,
, 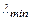 – максимальное и минимальное собственные числа матрицы.
– максимальное и минимальное собственные числа матрицы.
Дата добавления: 2015-11-24; просмотров: 1136;
