Прямые и итерационные методы.
Часть 2. системЫ линейных
АлгебраичЕских уравнений
Лекция 2
ПРЯМЫЕ МЕТОДЫ
ЦЕЛЬ ЛЕКЦИИ: Определить два класса численных методов (прямые и итерационные); показать, как строятся прямые методы Гаусса, LU-факторизации, Холесского; выполнить оценку их эффективности.
Постановка задачи.
Основная задача вычислительной алгебры – решение систем линейных алгебраических уравнений (СЛАУ)
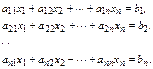
В дальнейшем будем использовать запись этой системы в компактной форме:
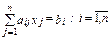
( запись 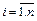 означает, что индекс i изменяется от 1 до n с шагом 1), или в векторном виде
означает, что индекс i изменяется от 1 до n с шагом 1), или в векторном виде
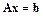 ,
,
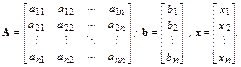 |
где
Предполагается, что матрица 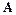 неособенная, т. е.
неособенная, т. е. 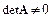 , и решение единственно.
, и решение единственно.
Прямые и итерационные методы.
Численные методы решения СЛАУ делятся на две большие группы: прямые и итерационные.
Прямые методы при отсутствии ошибок округления за конечное число арифметических операций позволяют получить точное решение 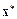 . В итерационных методах задается начальное приближение
. В итерационных методах задается начальное приближение 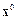 и строится последовательность
и строится последовательность
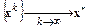 ,
,
где k – номер итерации. В действительности итерационный процесс прекращается, как только 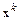 становится достаточно близким к
становится достаточно близким к 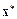 .
.
Имеется промежуточный класс методов, в которых решение ищется итерационно, однако для них заранее известно, какое число итераций необходимо выполнить, чтобы в отсутствии ошибок округления получить точное решение. На практике при вычислении приближенного решения число итераций в наиболее эффективных методах оказывается значительно меньшим, чем этого требует теория точного решения.
Какой класс методов лучше? Однозначно на этот вопрос ответить нельзя. Итерационные методы привлекательнее с точки зрения объема вычислений и требуемой памяти, когда решаются системы с матрицами высокой размерности. При небольших порядках системы используют прямые методы либо прямые методы в сочетании с итерационными методами.
Метод Гаусса.
В методе Гаусса линейная система
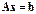
решается в два этапа. На первом этапе система 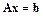 преобразуется к виду (см. рис. 2.1)
преобразуется к виду (см. рис. 2.1)
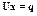 ,
,
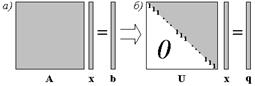 |
Рис. 2.1. Структура системы и портрет ее ненулевых элементов до (а) и после (б)
прямого хода Гаусса
где 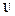 – верхняя треугольная матрица с единичной диагональю (это так
– верхняя треугольная матрица с единичной диагональю (это так
называемый прямой ход Гаусса). На втором этапе (обратный ход Гаусса) решается система 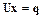 . Рассмотрим эти этапы подробнее.
. Рассмотрим эти этапы подробнее.
Прямой ход. Прямой ход Гаусса состоит из n шагов.
Первый шаг. Полагаем, что 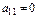 и разделим на него первое уравнение. Перепишем систему с учетом этого преобразования:
и разделим на него первое уравнение. Перепишем систему с учетом этого преобразования:
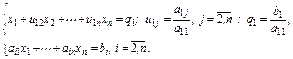
Умножим первое уравнение на 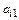 и вычтем его из i-го уравнения преобразованной системы:
и вычтем его из i-го уравнения преобразованной системы:
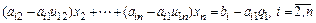
Обозначим 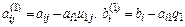 . Получим
. Получим
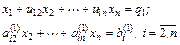
Второй шаг. На втором шаге из системы
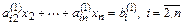
исключается 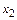 аналогичным образом:
аналогичным образом:
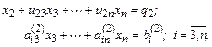
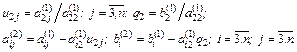
K-й шаг. Запишем общий вид преобразованной системы после k-го шага прямого хода Гаусса:
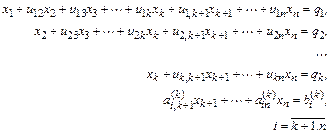
Здесь
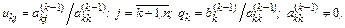
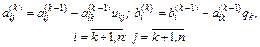
Проиллюстрируем, как меняется матрица системы в процессе прямого хода Гаусса на примере системы четвертого порядка (рис. 2.2; ненулевые элементы матрицы обозначены крестиками).
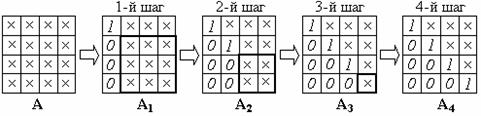
Рис. 2.2. Преобразование матрицы системы 4-го порядка на прямом ходе Гаусса
Оценим количество длинных операций (умножений и делений) на первом шаге прямого хода Гаусса. Преобразование первого уравнения требует n таких операций. Преобразование остальных n-1 уравнений – n(n-1) операций умножения и деления. Таким образом, первый шаг выполняется за 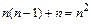 длинных операций. Рассуждая по аналогии, нетрудно найти затраты на остальных n-1 шагах. Суммарные затраты прямого хода Гаусса определяются в итоге рядом
длинных операций. Рассуждая по аналогии, нетрудно найти затраты на остальных n-1 шагах. Суммарные затраты прямого хода Гаусса определяются в итоге рядом
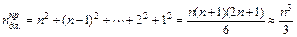 .
.
Последняя оценка имеет место для n>>1.
Обратный ход. Запишем систему, решаемую на обратном ходе, в координатном виде
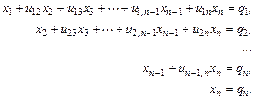
Ее решение:
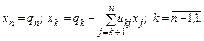
Запись 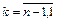 означает, что индекс k изменяется от значения n-1 до 1 с шагом 1.
означает, что индекс k изменяется от значения n-1 до 1 с шагом 1.
Требуемое число длинных операций на обратном ходе
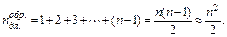
Приближенная оценка справедлива для n>>1.
Общие затраты метода Гаусса:
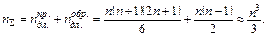
Таким образом, при больших n основные затраты в методе Гаусса приходятся на прямой ход.
Дата добавления: 2015-11-24; просмотров: 3227;
