Производная, правила и формулы дифференцирования

Пусть функция y = f(x) определена в промежутке X. Производной функции y = f(x) в точке х_o называется предел

= .

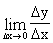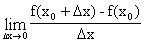Если этот предел конечный, то функция f(x) называется дифференцируемой в точке x_o; при этом она оказывается обязательно и непрерывной в этой точке.

Если же рассматриваемый предел равен ¥ (или - ¥), то при условии, что функция в точке х_o непрерывна, будем говорить, что функция f(x) имеет в точке х_o бесконечную производную.

Производная обозначается символами

y ¢, f ¢(x_o), , .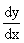

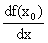Нахождение производной называется дифференцированием функции. Геометрический смысл производной состоит в том,что производная есть угловой коэффициент касательной к кривой y=f(x) в данной точке х_o; физический смысл - в том, что производная от пути по времени есть мгновенная скорость движущейся точки при прямолинейном движении s = s(t) в момент t_o.

Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

1) (с) ' = 0, (cu) ' = cu';

2) (u+v)' = u'+v';

3) (uv)' = u'v+v'u;

4) (u/v)' = (u'v-v'u)/v^2;

5) если y = f(u), u = j(x), т.е. y = f(j(x)) - сложная функция, или суперпозиция, составленная из дифференцируемых функций j и f, то 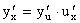, или

;

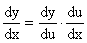6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем 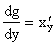¹ 0, то .

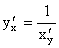На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций.

1. (u^m)' = m u^m-1 u' (m Î R).

2. (a^u)' = a^u lna× u'.

3. (e^u)' = e^u u'.

4. (log_a u)' = u'/(u ln a).

5. (ln u)' = u'/u.

6. (sin u)' = cos u× u'.

7. (cos u)' = - sin u× u'.

8. (tg u)' = 1/ cos²u× u'.

9. (ctg u)' = - u' / sin²u.

10. (arcsin u)' = u' / .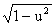

11. (arccos u)' = - u' / .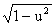

12. (arctg u)' = u'/(1 + u²).

13. (arcctg u)' = - u'/(1 + u²).

Вычислим производную степенно-показательного выражения y=u^v, (u>0), где u и v суть функции от х, имеющие в данной точке производные u', v'.

Прологарифмировав равенство y=u ^v, получим ln y = v ln u.

Приравнивая производные по х от обеих частей полученного равенства с помощью правил 3, 5 и формулы для производной логарифмической функции, будем иметь:

y'/y = vu'/u +v' ln u, откуда y' = y (vu'/u +v' ln u).

Итак,

(u ^v)'=u ^v (vu'/u+v' ln u), u > 0.

Например, если y = x ^{sin x}, то y' = x ^{sin x} (sin x/x + cos x× ln x).

Если функция y = f(x) дифференцируема в точке x, т.е. имеет в этой точке конечную производную y', то 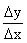= y'+a, где a®0 при Dх® 0; отсюда D y = y' Dх + a x.

Главная часть приращения функции, линейная относительно Dх, называется дифференциалом функции и обозначается dy: dy = y' Dх. Если положить в этой формуле y=x, то получим dx = x'Dх = 1×Dх =Dх, поэтому dy=y'dx, т. е. символ для обозначения производной 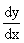можно рассматривать как дробь.

Приращение функции D y есть приращение ординаты кривой, а дифференциал dy есть приращение ординаты касательной.

Пусть мы нашли для функции y=f(x) ее производную y ¢= f ¢(x). Производная от этой производной называется производной второго порядка функции f(x), или второй производной, и обозначается .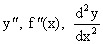

Аналогично определяются и обозначаются:

производная третьего порядка - ,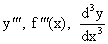

производная четвертого порядка -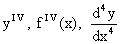

и вообще производная n-го порядка - .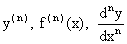

Пример 3.15. Вычислить производную функции y=(3x³-2x+1)×sin x.

Решение. По правилу 3, y'=(3x³-2x+1)'×sin x + (3x³-2x+1)×(sin x)' =
= (9x²-2)sin x + (3x³-2x+1)cos x.

Пример 3.16. Найти y', y = tg x + .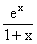

Решение. Используя правила дифференцирования суммы и частного, получим: y'=(tgx + 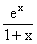)' = (tgx)' + ( )' = + = .

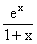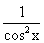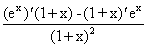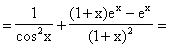
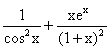Пример 3.17. Найти производную сложной функции y= ,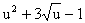
u=x⁴ +1.

Решение. По правилу дифференцирования сложной функции, получим: y'_x =y '_u u'_x =( 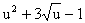)'_u(x⁴ +1)'_x =(2u + 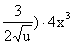. Так как u=x⁴ +1,то
(2 x⁴ +2+ .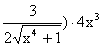

Пример 3.18. Найти производную функции y= .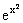

Решение. Представим функцию y= 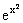в виде суперпозиции двух функций: y = e^u и u = x². Имеем: y'_x =y '_u u'_x = (e^u)'_u(x²)'_x = e^u ×2x. Подставляя x² вместо u, получим y=2x .

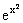Пример 3.19. Найти производную функции y=ln sin x.

Решение. Обозначим u=sin x, тогда производная сложной функции y=ln u вычисляется по формуле y' = (ln u)'_u(sin x)'_x= .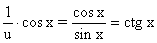

Пример 3.20. Найти производную функции y= .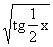

Решение. Случай сложной функции, полученной в результате нескольких суперпозиций, исчерпывается последовательным применением правила 5:

.

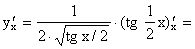
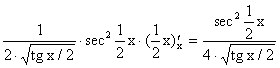Пример 3.21. Вычислить производную y=ln .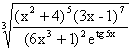

Решение. Логарифмируя и используя свойства логарифмов, получим:

y=5/3ln(x²+4) +7/3ln(3x-1)-2/3ln(6x³+1)-1/3tg 5x.

Дифференцируя обе части последнего равенства, получим:

.

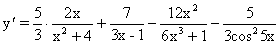Экстремум функции

Функция y=f(x) называется возрастающей (убывающей) в некотором интервале, если при x₁< x₂ выполняется неравенство f(x₁) < f (x₂) (f(x₁) > f(x₂)).

Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f ¢(x) > 0 (f ¢(x) < 0).

Точка x_о называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки x_о, для всех точек которой верно неравенство f(x) £ f(x_о) (f(x) ³ f(x_о)).

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.

Необходимые условия экстремума. Если точка x_о является точкой экстремума функции f(x), то либо f ¢(x_о) = 0, либо f ¢(x_о) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x_о - критическая точка. Если f ¢ (x) при переходе через точку x_о меняет знак плюс на минус, то в точке x_о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x_о экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную
f ¢ (x) в окрестности точки x_о и вторую производную 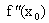в самой точке x_о. Если f ¢(x_о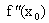) = 0, >0 ( 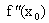<0), то точка x_о является точкой локального минимума (максимума) функции f(x). Если же 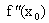=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

Пример 3.22.Найти экстремумы функции f(x) = 2x³ - 15x²+ 36x - 14.

Решение. Так как f ¢ (x) = 6x² - 30x +36 = 6(x -2)(x - 3), то критические точки функции x₁ = 2 и x₂ = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x₁ = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x₂ = 3 производная меняет знак минус на плюс, поэтому в точке x₂ = 3 у функции минимум. Вычислив значения функции в точках x₁ = 2 и x₂ = 3, найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) = 13.

Пример 3.23.Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, а четвертой стороной примыкала к стене. Для этого имеется a погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?

Решение. Обозначим стороны площадки через x и y. Площадь площадки равна S = xy. Пусть y - это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2x + y = a. Поэтому y = a - 2x и S = x(a - 2x), где 0 £ x £ a/2 (длина и ширина площадки не могут быть отрицательными). S ¢ = a - 4x, a - 4x = 0 при x = a/4, откуда
y = a - 2×a/4 =a/2. Поскольку x = a/4 - единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. При x < a/4 S ¢ >0, а при x >a/4 S ¢ <0, значит, в точке x=a/4 функция S имеет максимум. Значение функции S(a/4) = a/4(a - a/2) = a² /8 (кв. ед).

Поскольку S непрерывна на [0, a/2] и ее значения на концах S(0) и S(a/2) равны нулю, то найденное значение будет наибольшим значением функции. Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является y = 2x.

Пример 3.24.Требуется изготовить закрытый цилиндрический бак вместимостью V=16p » 50 м³. Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?

Решение. Площадь полной поверхности цилиндра равна S = 2pR(R+Н). Мы знаем объем цилиндра V = pR²Н Þ Н = V/pR² =16p/ pR² = 16/ R². Значит, S(R) = 2p(R²+16/R). Находим производную этой функции:
S ¢(R) = 2p(2R- 16/R²) = 4p (R- 8/R²). S ¢(R) = 0 при R³ = 8, следовательно,
R = 2, Н = 16/4 = 4.