Вероятность безотказной работы

Вероятность безотказной работы - вероятность того, что в переделах заданной наработки отказа объекта не возникнет. В свою очередь наработка - продолжительность или объем работы объекта.

Обозначим вероятность безотказной работы Р(t). Пуст t –время, в течение которого необходимо определить вероятность безотказной работы (заданное время); Т₁ - время работы аппаратуры от ее включения до отказа.

Тогда согласно определению

Р(t) = Р(Т₁≥ t) (2-1)

Т.е. вероятность того, что время Т₁ от момента включения аппаратуры до его отказа будет больше или равно времени t , в течении которого определяется вероятность безотказной работы. Р(t) есть функция времени.

Основные свойства функции Р(t).

1. Является убывающей функцией времени.

2. 0 ≤ P(t) ≤ 1.

3. Р(0) = 1, Р(∞) = 0.

Характерный вид функции приведен на рис.2.

Практически, значение Р(t) определяется из статистических данных следующей оценкой.

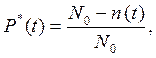(2-2)

где N₀- число объектов в начале испытаний;

п(t)- число отказавших объектов за время t. При .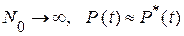

На практике, иногда более удобной характеристикой является вероятность неисправной работы или вероятность отказов.

Так как отказ и исправная работа есть события несовместные, то

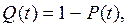(2-3)

или согласно определению

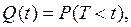(2-4)

Из этого выражения видно, что вероятность отказа является интегральной функцией (интегральным законом) распределения времени работы Т₁ до отказа.

Тогда

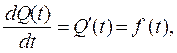(2-5)

т.е. производная от вероятности отказа есть дифференциальный закон распределения времени работы аппаратуры до ее отказа.

Выражение для статистического определения отказа получим из (2-2) и (2-3).

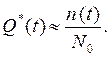(2-6)

Вид функций Р(t) и Q(t) представлен на рис.3.

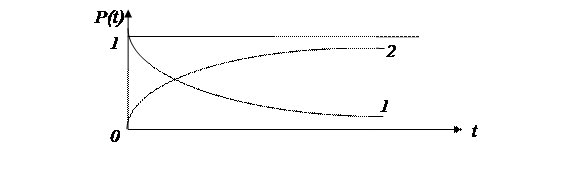
1 – P(t), 2 – Q(t).

Рис. 3. Вид функции P(t) и Q(t).