Плоскость в пространстве
Всякое уравнение первой степени относительно координат 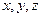
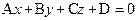 (3.1)
(3.1)
задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.
Вектор 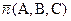 , ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.
, ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.
Особые случаи уравнения (3.1):
1. 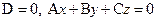 ‑ плоскость проходит через начало координат.
‑ плоскость проходит через начало координат.
2. 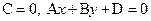 ‑ плоскость параллельна оси Oz.
‑ плоскость параллельна оси Oz.
3. 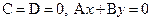 ‑ плоскость проходит через ось Oz.
‑ плоскость проходит через ось Oz.
4. 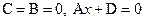 ‑ плоскость параллельна плоскости Oyz.
‑ плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей: 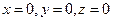 .
.
Пример 1.15. Cоставьте уравнение плоскости, зная, что точка 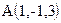 служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Решение. По условию задачи вектор 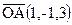 является нормальным вектором плоскости, тогда ее уравнение можно записать в виде
является нормальным вектором плоскости, тогда ее уравнение можно записать в виде 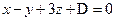 . Подставив координаты точки
. Подставив координаты точки 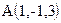 , принадлежащей плоскости, найдем D:
, принадлежащей плоскости, найдем D:  . Итак,
. Итак, 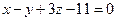 .
.
Пример 1.16. Составьте уравнение плоскости, проходящей через ось Оz и образующей с плоскостью 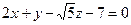 угол 60о.
угол 60о.
Решение. Плоскость, проходящая через ось Oz, задается уравнением 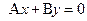 , где А и В одновременно не обращаются в нуль. Пусть В не равно 0,
, где А и В одновременно не обращаются в нуль. Пусть В не равно 0, 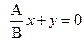 . По формуле косинуса угла между двумя плоскостями
. По формуле косинуса угла между двумя плоскостями
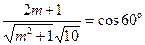 , где
, где 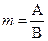 .
.
Решая квадратное уравнение 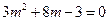 , находим его корни
, находим его корни  ,
, 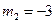 , откуда получаем две плоскости
, откуда получаем две плоскости 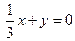 и
и 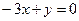 .
.
Дата добавления: 2015-12-22; просмотров: 958;
