Векторы в евклидовом пространстве

Элементы векторной алгебры

Векторы в евклидовом пространстве

В отличие от скалярных величин, которые полностью характеризуются своим численным значением в выбранной системе единиц (температура, работа, плотность и т.д.), векторные величины, кроме численного значения, обладают также направлением в пространстве (например, сила и скорость).

Из школьного курса математики известно, что вектор можно изобразить направленным отрезком, т.е. отрезком прямой, для которого указано какая точка, является началом и какая концом, и при этом указать единицу масштаба (рис. 1.1).

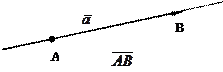
Рис. 1.1

Если точка Аначало, а Вконец вектора, то вектор записывается в виде 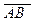или .

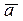Численная величина вектора называется модулем вектора. Иногда модуль вектора называют его длиной. Модуль, или длина вектора обозначается как | |, | |.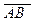

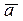Вектор, у которого начало совпадает с концом, называется нулевым. Векторы, расположенные на прямой или параллельных прямых, называются коллинеарнымии обозначаются 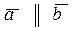. Векторы, лежащие на параллельных плоскостях или на одной и той же плоскости, называются компланарными.

.