Векторное произведение двух векторов

Векторным произведением вектора 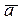на вектор 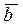называется новый вектор 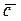, обозначаемый символом

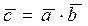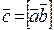или (1.7.1)

и определяемый следующими тремя условиями:

1) Модуль вектора 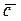равен площади параллелограмма, построенного на векторах 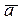и 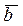(после совмещения их начал), т.е.

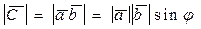, (1.7.2)

где 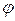- угол между векторам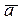и и 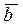(рис.1.11).

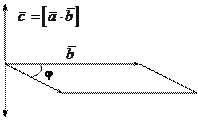
Рис.1.11

2). Вектор 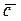перпендикулярен к плоскости этого параллелограмма (т.е. перпендикулярен обоим векторам 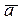и ).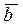

3). Вектор 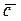направлен в ту сторону от этой плоскости, что кратчайший поворот от вектора 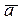к вектору 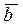вокруг вектора 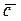(после смещения начал всех трех векторов) кажется происходящим против часовой стрелки, если смотреть из конца вектора 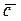. Векторы 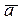, , 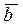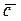образуют правую тройку векторов.

Замечание.Правую тройку образуют, например, большой, указательный, и средний пальцы правой руки; при пользовании левой системой координат в определении векторного произведения вместо правой берут левую тройку , , .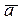

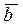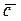Своим прообразом произведение двух векторов имеет в механике операцию отыскания момента силы относительно точки. Именно, если в некоторой точке А приложена сила , то момент 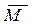этой силы относительно определенной точки О есть вектор, который в принятом нами обозначении (1.7.1) должен быть записан в ви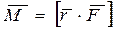де , где 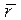- вектор, идущий из точки О в точку А.