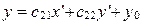Преобразование аффинной системы координат
Возьмем на плоскости две аффинные системы координат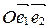 
и 
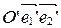. Первую назовем старой, вторую - новой. Пусть М – произвольная точка плоскости, которая в старой системе 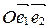имеет координаты х,у, а в новой системе 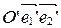- координаты 
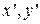(рис. 39).
Задача преобразования координат состоит в следующем: зная координаты нового начала и новых координатных векторов в старой системе:
, 
, 
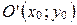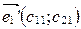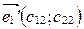,(3)
выразить координаты х,у точки М в старой системе координат, через координаты 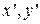этой точки в новой системе.
Из формул (3) следует, что
; 
; 
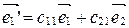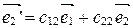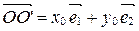. (4)
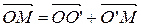(по правилу треугольника).
Так как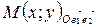 
, 
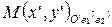, то по определению координат точки 
, 
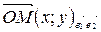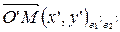, т.е. 
; 
.
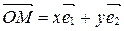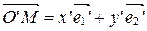Тогда, используя формулы (4), получим:
,
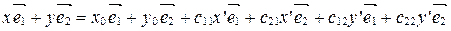т.е.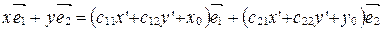 
,
откуда находим:
 ;
|
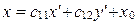. Так выражаются координаты х,у произвольной точки М в старой системе 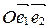через ее координаты 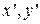в новой системе .
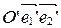Формулы (5) называются формулами преобразования аффинной системы координат.
Коэффициенты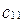 
, 
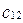при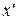 
- координаты нового вектора 
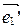в старой системе 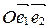; коэффициенты , 
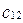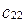при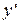 
- координаты нового вектора 
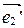в старой системе, свободные члены 
, 
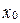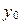- координаты нового начала 
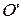в старой системе:
Координаты точки М
в новой системе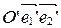
Таблица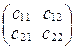 
называется матрицей перехода от базиса 
, 
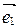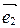к базису , .
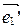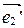Дата добавления: 2015-11-28; просмотров: 2509;