В аффинной системе координат

Плоскость 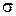в пространстве можно задать точкой и двумя неколлинеарными векторами, параллельными ей (или принадлежащими ей) или тремя точками, не лежащими на одной прямой. В первом случае этот факт будем обозначать так: 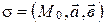; во втором – .

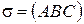Пусть в пространстве дана аффинная система координат .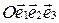

1. Уравнение плоскости, заданной точкой и двумя неколлинеарными векторами.

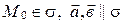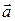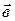Пусть , || (рис. 65), 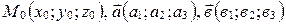в системе .

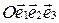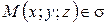тогда и только тогда, когда векторы 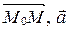и 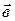компланарны, т.е. их смешанное произведение 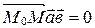. Переходя к координатам, получим уравнение:

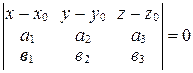. (20)

Итак, если 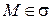, то ее координаты удовлетворяют уравнению (20). Если 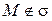, то векторы 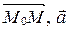и 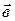некомпланарны, следовательно, координаты точки 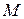не удовлетворяют уравнению (20). Таким образом, уравнение (20) есть уравнение плоскости 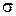. Оно называется

уравнением плоскости, заданной точкой 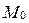и двумя неколлинеарными векторам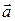и и .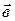

2. Параметрическое уравнение плоскости.

Пусть , .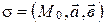

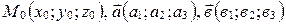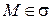тогда и только тогда, когда векторы 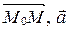и 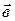компланарны. По теореме о компланарных векторах 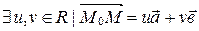. Переходя к координатам, получаем: 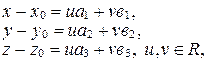или

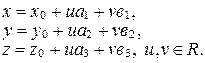(21)

Система уравнений (21) называется параметрическим уравнением плоскости.

Действительные числа u и v называются параметрами.

Геометрический смысл параметров u и v: для любой точки 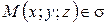существует единственная пара параметров 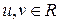, удовлетворяющих уравнениям (21), и обратно, 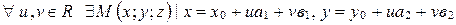и .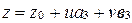

3. Уравнение плоскости, заданной тремя точками.

Пусть 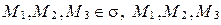не лежат на одной прямой, , , .

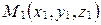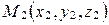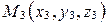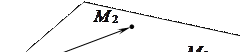
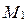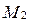Так как точки , и 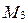не лежат на одной прямой, то 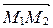|| 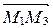(рис. 66). Следовательно, плоскость 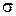можно задать точкой 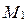и двумя неколлинеарными векторам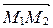и и 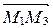: 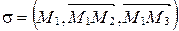. Применяя уравнение (20), получаем:

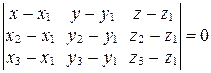. (22)

Уравнение (22) называется уравнением плоскости, заданной тремя точками .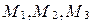

4. Уравнение плоскости «в отрезках».

Пусть 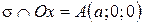, , 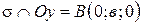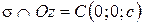(рис. 67), где .

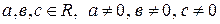Используя уравнение (22), получим:

;

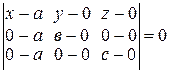т.е. .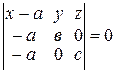

Раскроем определитель, стоящий в левой части, и преобразуем это выражение:

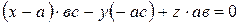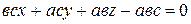; ; разделим обе части этого уравнения на 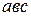: 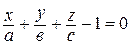, откуда получаем уравнение:

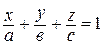. (23)

Уравнение (23) называется уравнением плоскости «в отрезках».

Геометрический смысл а, в и с: а – это абсцисса точки пересечения плоскости 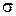с осью 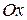, в – ордината точки пересечения 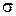с осью 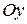, с - аппликата точки пересечения 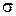с осью аффинной системы координат.