Задания для самостоятельной работы. 1. Какие из векторов параллельны плоскости и почему?
1. Какие из векторов 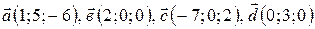 параллельны плоскости
параллельны плоскости 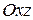 и почему?
и почему?
2. Справедливы ли утверждения, доказанные в пунктах 1-13, если уравнение плоскости задано в прямоугольной декартовой системе координат и почему?
3. Составьте уравнение плоскости, проходящей через точку 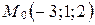 и параллельной плоскости: а)
и параллельной плоскости: а) 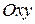 ; б)
; б) 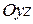 ; в)
; в) 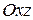 (пользуясь частными случаями общего уравнения плоскости).
(пользуясь частными случаями общего уравнения плоскости).
4. Составьте уравнение плоскости, которая проходит через точку 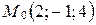 и содержит: а) ось
и содержит: а) ось 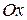 ; б) ось
; б) ось 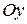 ; в) ось
; в) ось 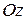 (пользуясь частными случаями общего уравнения плоскости).
(пользуясь частными случаями общего уравнения плоскости).
§ 23. Основные аффинные задачи,
связанные с плоскостью (обзор)
1. Взаимное расположение двух плоскостей.
Выяснить взаимное расположение двух плоскостей позволяет следующая теорема:
Теорема 1. Пусть в аффинной системе координат 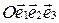 плоскости
плоскости 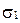 и
и 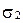 заданы общими уравнениями:
заданы общими уравнениями:
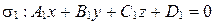 ,
,
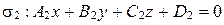 .
.
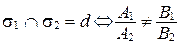 или
или 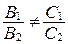 ;
;
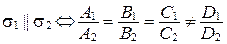 (коэффициенты при х, у, z пропорциональны, а свободные члены им не пропорциональны);
(коэффициенты при х, у, z пропорциональны, а свободные члены им не пропорциональны);
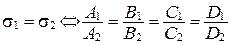 .
.
2. Взаимное расположение трех плоскостей.
Вопрос о взаимном расположении трех плоскостей 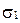 ,
, 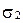 и
и 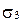 сводится к исследованию вопроса о взаимном расположении трех пар плоскостей:
сводится к исследованию вопроса о взаимном расположении трех пар плоскостей: 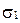 и
и 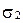 ,
, 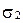 и
и 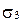 ,
, 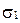 и
и 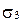 .
.
Возможны восемь случаев взаимного расположения этих плоскостей:
1) 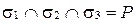 (рис. 69, а);
(рис. 69, а);
2) 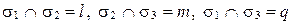 (рис. 69, б);
(рис. 69, б);
3) 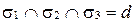 (рис. 69, в);
(рис. 69, в);
4) 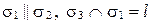 (следовательно,
(следовательно, 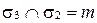 ) (рис. 69, г);
) (рис. 69, г);
5) 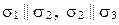 (следовательно,
(следовательно, 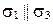 ) (рис. 69, д);
) (рис. 69, д);
6) 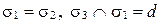 (рис. 69, е);
(рис. 69, е);
7) 
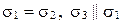 (рис. 69, ж);
(рис. 69, ж);
8) 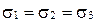 (рис. 69, з).
(рис. 69, з).

3. Геометрический смысл знака многочлена 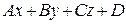 .
.
Теорема 2. Если в аффинной системе координат плоскость 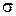 задана уравнением
задана уравнением 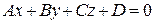 , то два полупространства, на которые эта плоскость разбивает пространство, определяются условиями
, то два полупространства, на которые эта плоскость разбивает пространство, определяются условиями
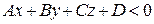 и
и 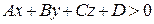 .
.
4. Пучок и связка плоскостей.
Пучком плоскостей называется множество всех плоскостей, проходящих через одну и ту же прямую 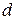 . Прямая
. Прямая 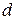 называется осью этого пучка.
называется осью этого пучка.
Пусть 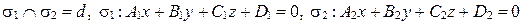 . Тогда уравнение пучка плоскостей с осью
. Тогда уравнение пучка плоскостей с осью 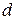 имеет вид:
имеет вид:
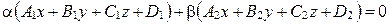 , где
, где 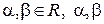 не равны нулю одновременно.
не равны нулю одновременно.
Связкой плоскостей называется множество всех плоскостей, проходящих через одну и ту же точку 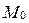 . Точка
. Точка 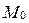 называется центром связки.
называется центром связки.
Пусть 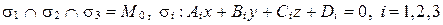 . Тогда уравнение связки плоскостей имеет вид:
. Тогда уравнение связки плоскостей имеет вид:
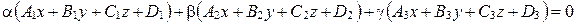 , где
, где 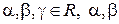 и
и 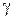 не равны нулю одновременно.
не равны нулю одновременно.
Дата добавления: 2015-11-28; просмотров: 799;
