Различные уравнения прямой в пространстве
Положение прямой в пространстве определяется полностью, если даны:
а) две ее точки;
б) точка и направляющий вектор;
в) две плоскости, пересекающиеся по этой прямой.
Пусть в пространстве выбрана аффинная система координат 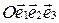 .
.
1. Каноническое уравнение прямой.
 Пусть прямая
Пусть прямая 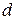 задана в пространстве точкой
задана в пространстве точкой 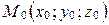 и направляющим вектором
и направляющим вектором 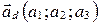 (рис. 73).
(рис. 73).
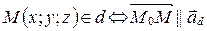 .
.
Далее применяем условие коллинеарности двух векторов в пространстве в координатах (см. § 5). При этом возможны различные случаи:
а) 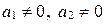 и
и  . Тогда получаем следующее уравнение прямой:
. Тогда получаем следующее уравнение прямой:
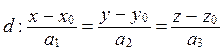 . (28)
. (28)
б) 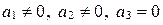 .
.
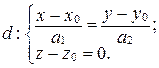 (29)
(29)
в) 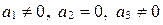 (запишите уравнение прямой
(запишите уравнение прямой 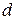 самостоятельно).
самостоятельно).
г) 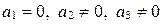 (запишите уравнение прямой
(запишите уравнение прямой 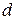 самостоятельно).
самостоятельно).
д) 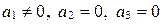 . Получаем следующее уравнение прямой
. Получаем следующее уравнение прямой 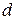 :
:
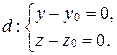 (30)
(30)
е) 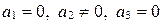 (запишите уравнение прямой
(запишите уравнение прямой 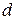 самостоятельно).
самостоятельно).
ж) 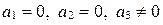 (запишите уравнение прямой
(запишите уравнение прямой 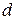 самостоятельно).
самостоятельно).
Уравнения (28)-(30) (а также уравнения, записанные вами в пунктах в), г), е) и ж)) называются каноническими уравнениями прямой в пространстве.
2. Уравнение прямой, заданной двумя точками.
Пусть 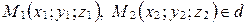 . Тогда прямую
. Тогда прямую 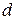 можно задать точкой
можно задать точкой 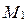 и направляющим вектором
и направляющим вектором 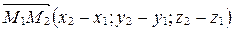 . Поэтому применяем каноническое уравнение прямой:
. Поэтому применяем каноническое уравнение прямой:
 . (31)
. (31)
Уравнение (31) называется уравнением прямой в пространстве, заданной двумя точками.
Если одна или две координаты вектора 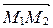 окажутся нулевыми, то применяем частные случаи канонического уравнения прямой, т.е. уравнения вида (29) или (30).
окажутся нулевыми, то применяем частные случаи канонического уравнения прямой, т.е. уравнения вида (29) или (30).
3. Параметрическое уравнение прямой.
В случае, когда прямая 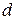 задана так же, как в пункте 1 (точкой
задана так же, как в пункте 1 (точкой 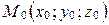 и направляющим вектором
и направляющим вектором 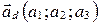 ), можно получить параметрическое уравнение прямой.
), можно получить параметрическое уравнение прямой. 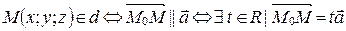 (по теореме о коллинеарных векторах). Переходя к координатам, получаем:
(по теореме о коллинеарных векторах). Переходя к координатам, получаем:
|
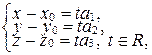
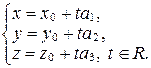 (32)
(32)
Система уравнений (32) называется параметрическим уравнением прямой в пространстве.
Действительное число 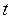 в системе (32) называется параметром и имеет такой же смысл, как и параметр
в системе (32) называется параметром и имеет такой же смысл, как и параметр 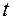 в параметрическом уравнении прямой на плоскости (см. § 15).
в параметрическом уравнении прямой на плоскости (см. § 15).
 4. Уравнение прямой, заданной двумя пересекающимися плоскостями.
4. Уравнение прямой, заданной двумя пересекающимися плоскостями.
Пусть 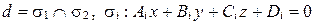 в
в 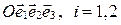 (рис. 74).
(рис. 74).
Точка 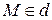 тогда и только тогда, когда ее координаты
тогда и только тогда, когда ее координаты 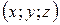 являются решением системы уравнений плоскостей
являются решением системы уравнений плоскостей 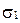 и
и 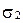 .
.
Система уравнений
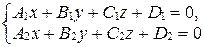 (33)
(33)
называется уравнением прямой, заданной двумя пересекающимися плоскостями.
Лемма 1. Вектор
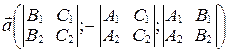 (34)
(34)
является направляющим вектором прямой 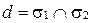 .
.
□ Воспользуемся дважды леммой о параллельности вектора и плоскости.
1) Докажем, что 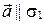 .
.
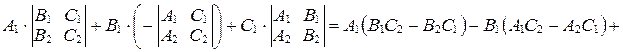
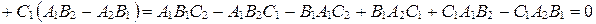 . Тогда по лемме о параллельности вектора и плоскости
. Тогда по лемме о параллельности вектора и плоскости 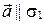 .
.
2) Докажите самостоятельно, что  .
.
Из пунктов 1) и 2) следует, что 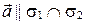 , т.е.
, т.е. 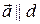 . ■
. ■
Итак, из леммы 1 следует, что если прямая 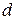 задана как линия пересечения двух плоскостей
задана как линия пересечения двух плоскостей 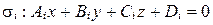 ,
, 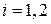 , то координаты ее направляющего вектора
, то координаты ее направляющего вектора 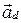 находятся по формуле (34).
находятся по формуле (34).
Замечание. Как и в случае прямой на плоскости, переменные  в уравнениях (28)-(33) называются текущими координатами точек прямой в пространстве.
в уравнениях (28)-(33) называются текущими координатами точек прямой в пространстве.
Дата добавления: 2015-11-28; просмотров: 1014;
