Задания для самостоятельной работы. 1. В аффинной системе координат задана прямая уравнением
1. В аффинной системе координат задана прямая уравнением 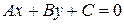 . Какая фигура определяется условием: а)
. Какая фигура определяется условием: а) 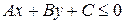 ; б)
; б) 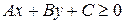 ?
?
2. Верно ли утверждение, что прямая 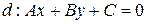 пересекает отрезок
пересекает отрезок 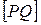 , где
, где 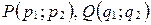 , тогда и только тогда, когда
, тогда и только тогда, когда 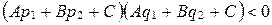 и почему?
и почему?
3. Даны треугольник 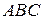 с вершинами
с вершинами 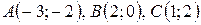 и прямая
и прямая 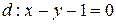 . Существует ли на прямой
. Существует ли на прямой 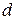 точки, являющиеся внутренними точками треугольника
точки, являющиеся внутренними точками треугольника 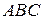 ?
?
4. Существуют ли значения коэффициентов А и В, при которых прямые, заданные уравнениями 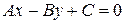 и
и 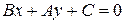 , параллельны?
, параллельны?
5. Какой вид имеет уравнение прямой, параллельной прямой 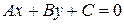 и проходящей через: а) начало координат; б) точку
и проходящей через: а) начало координат; б) точку 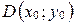 ?
?
6. Дано уравнение пучка прямых 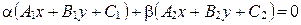 . Докажите, что прямые
. Докажите, что прямые 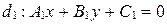 и
и  принадлежат этому пучку.
принадлежат этому пучку.
Лекция 10
Прямая в прямоугольной декартовой
Системе координат
Уравнение прямой, заданной точкой и
Вектором нормали
Ненулевой вектор называется перпендикулярным данной прямой, если он ортогонален любому направляющему вектору этой прямой.
Вектор, перпендикулярный прямой, называется вектором нормали этой прямой или ее нормальным вектором. Для каждой прямой на плоскости существует бесконечное множество векторов нормали. Любые два из них коллинеарны (рис. 60).
Вектор нормали прямой 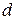 будем обозначать через
будем обозначать через 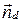 .
.
 |  |
Лемма 1. Если прямая 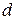 в прямоугольной системе координат
в прямоугольной системе координат 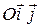 задана уравнением
задана уравнением 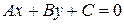 , то вектор
, то вектор 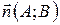 перпендикулярен прямой
перпендикулярен прямой 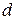 .
.
□ Возьмем направляющий вектор 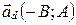 прямой
прямой 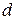 и найдем скалярное произведение
и найдем скалярное произведение 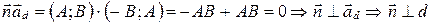 . ■
. ■
Следствие. Уравнение прямой 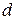 , заданной в прямоугольной декартовой системе координат точкой
, заданной в прямоугольной декартовой системе координат точкой 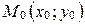 и вектором нормали
и вектором нормали 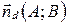 , имеет вид
, имеет вид 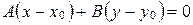 .
.
□ Если 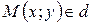 , то
, то 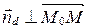 (рис. 61) Þ
(рис. 61) Þ 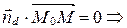
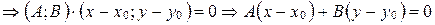 .
.
Если 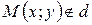 , то вектор
, то вектор 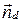 не ортогонален вектору
не ортогонален вектору 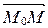 , т.е.
, т.е. 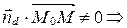
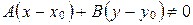 .
.
Итак, доказано, что точка 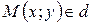 тогда и только тогда, когда ее координаты удовлетворяют уравнению
тогда и только тогда, когда ее координаты удовлетворяют уравнению
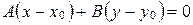 . ■ (19)
. ■ (19)
Уравнение (19) называется уравнением прямой, заданной точкой и вектором нормали.
Замечание. Если в прямоугольной декартовой системе координат прямая 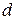 задана общим уравнением
задана общим уравнением 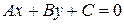 , то геометрический смысл коэффициентов при х и у состоит в следующем: А и В есть координаты вектора нормали прямой
, то геометрический смысл коэффициентов при х и у состоит в следующем: А и В есть координаты вектора нормали прямой 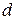 , т.е.
, т.е. 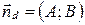 .
.
Дата добавления: 2015-11-28; просмотров: 804;
