Общее уравнение прямой и его частные случаи

Докажем следующую теорему об общем уравнении прямой:

Теорема 1. Любая прямая на плоскости задается в аффинной системе координат уравнением первой степени с двумя неизвестными 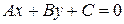, где А и В не равны 0 одновременно. Обратно, линия на плоскости, заданная в аффинной системе координат уравнением первой степени 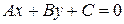(где А и В не равны 0 одновременно), есть прямая. Вектор 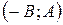является направляющим вектором этой прямой.

□ Пусть 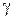- прямая, 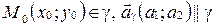. Запишем каноническое уравнение прямой :

.

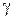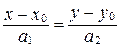Преобразуем его: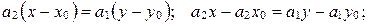

.

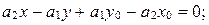
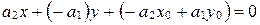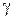Положим . Тогда уравнение прямой имеет вид:

.

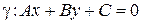Так как 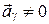(по определению), то 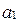и не равны 0 одновременно, следовательно, А и В не равны 0 одновременно.

Докажем обратное утверждение. Пусть некоторая линия 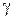задана в аффинной системе координат на плоскости уравнением 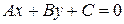, где 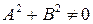. Докажем, что 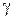- прямая.

Найдем уравнение прямой 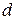, заданной точкой 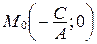и направляющим вектором , где А, В и С взяты из уравнения линии :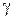

.

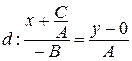Преобразуем это уравнение: . Итак, 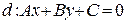, причем 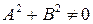, т.к. .

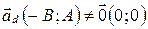Уравнение прямой 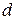в точности совпадает с уравнением линии 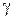, следовательно, 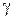совпадает с 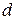, т.е. 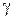есть прямая.

Так как вектор 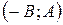является направляющим вектором прямой 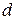, а 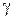совпадает с 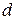, то 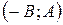- направляющий вектор прямой . ■

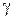Уравнение 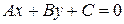называется общим уравнением прямой;

х и у – текущие координаты произвольной точки прямой.