Повторение испытаний

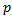Пусть производится независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Условимся считать, что вероятность события А в каждом испытании одна и та же, и равна . Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна .

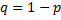Поставим перед собой задачу вычислить вероятность того, что при испытаниях событие А осуществится ровно 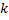раз и, следовательно, не осуществится 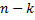раз, причём совсем не требуется, чтобы событие А повторилось ровно 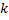раз в определённой последовательности. Такая вероятность обозначается .

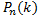Формула Бернулли

Поставленную задачу можно решить с помощью так называемой формулы Бернулли. Вероятность сложного события, состоящего в том, что в испытаниях событие А наступит 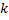раз и не наступит 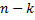раз, по теореме умножения вероятностей независимых событий равна 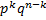. Таких сложных событий может быть столько, сколько можно составить 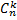. Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. А так как вероятности этих сложных событий одинаковы, то искомая вероятность равна вероятности одного сложного события, умноженной на их число: .

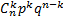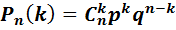
Полученная формула называется формулой Бернулли.