Аксиоматическое определение вероятности
Пусть 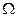 - пространство элементарных исходов,
- пространство элементарных исходов, 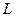 - некоторое множество (система ) случайных событий.
- некоторое множество (система ) случайных событий.
Определение.Система 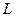 случайных событий называется алгеброй событий, если выполнены условия: 1)
случайных событий называется алгеброй событий, если выполнены условия: 1) 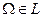 ; 2) если
; 2) если 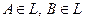 , то
, то 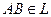 ,
, 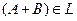 ,
, 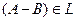 .
.
Из этого определения вытекает, что 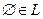 ,
, 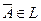 .
.
Определение.Алгебра событий называется 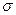 - алгеброй, если из того, что
- алгеброй, если из того, что 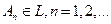 , следует
, следует 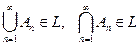 .
.
Определение. Числовая функция 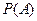 , определенная на алгебре событий
, определенная на алгебре событий 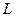 , называется вероятностью, если выполнены следующие аксиомы.
, называется вероятностью, если выполнены следующие аксиомы.
Аксиома 1. Каждому событию 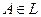 ставится в соответствие неотрицательное число
ставится в соответствие неотрицательное число 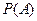 - его вероятность, т.е.
- его вероятность, т.е. 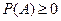 для любого
для любого 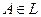 .
.
Аксиома 2.Вероятность достоверного события равна единице: 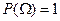 .
.
Аксиома 3. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, т.е. 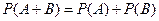 , если
, если 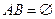 .
.
Аксиома 4. Для любой последовательности событий из 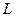 такой, что
такой, что 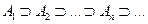 и
и 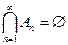 , справедливо равенство
, справедливо равенство 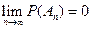 .
.
Определение.Тройка 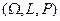 , в которой
, в которой 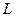 является
является 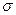 - алгеброй и функция
- алгеброй и функция 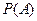 удовлетворяет аксиомам 1-4, называется вероятностным пространством.
удовлетворяет аксиомам 1-4, называется вероятностным пространством.
Простейшие следствия из аксиом вероятности:
1. Сумма вероятностей противоположных событий равна единице: 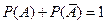 . Тогда
. Тогда 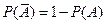 .
.
2. Вероятность невозможного события равна нулю: 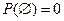 .
.
3. Если событие A влечет событие B 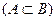 , то
, то 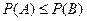 .
.
4. Для любых событий A и B верны соотношения: 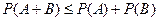 и
и 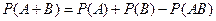 (Теорема сложения вероятностей).
(Теорема сложения вероятностей).
5. Для любых событий 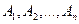 выполняется неравенство
выполняется неравенство 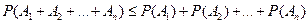 .
.
6. Если события 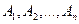 попарно несовместны (т.е.
попарно несовместны (т.е. 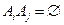 при любых
при любых 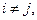
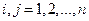 ), то
), то 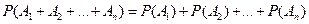 .
.
7. Если события 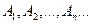 - попарно несовместны и
- попарно несовместны и 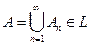 , то
, то 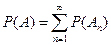 .
.
8. Если 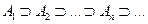 и
и 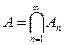 , то
, то 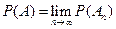 .
.
Если 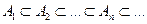 и
и 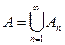 , то
, то 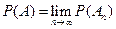 .
.
Дата добавления: 2016-01-09; просмотров: 1868;
