Операции над событиями. Пространство элементарных исходов - есть произвольное множество, а случайные события – его подмножества

Пространство элементарных исходов 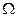- есть произвольное множество, а случайные события – его подмножества. Введем операции над событиями и свяжем с ними операции над множествами.

Определение.Если при каждом осуществлении комплекса условий, при котором происходит событие A, происходит и событие B, то говорят, что A влечет за собой B, или A является частным случаем B (обозначается 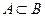). В этом случае, множество A является подмножеством множества B.

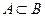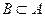Определение.Если и , то говорят, что события A и B равны: 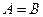. В этом случае, множества A и B совпадают.

Определение.Суммой или объединением двух событий A и B называется событие (обозначается 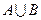или 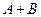), состоящее в появлении хотя бы одного из них.

По индукции определяется сумма n событий:

.

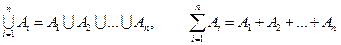Операции сложения событий соответствует операция объединения множеств.

Определение.Произведением или пересечением двух событий A и B называется событие (обозначается 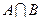или 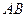), состоящее в том, что они произошли одновременно.

По индукции произведение n событий: 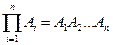, 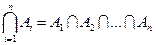означает событие, состоящее в появлении всех событий .

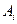Операции перемножения событий соответствует оперция пересечения множеств.

Понятия суммы и произведения событий распространяются на бесконечные последовательности событий, в этих случаях соответственно применяют обозначения:

, .

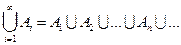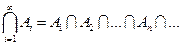Определение.Разностью событий A и B называется событие (обозначается 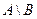или 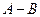), которое означает, что наступает событие A и не происходит событие B. Разность множеств A и B соответствует разности событий.

Определение.Событие 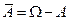называют противоположным событию A; событие 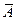означает, что A не произошло. Множество, соответсвующее событию 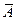, является дополнением к множеству A.

Определение.События A и B называют несовместными, если в результате эксперимента они не могут произойти одновременно, т.е. 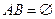. Это соотношение означает, что множества A и B не пересекаются.

Пример.Эксперимент состоит в подбрасывании игральной кости один раз.

Элементарный исход 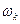={на верхней грани выпало к очков}. Пространство элементарных исходов 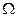состоит из шести элементов: 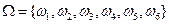. Рассмотрим события из примера 1:

А={выпало 5 очков}, B={число выпавших очков четное}.

Эти события рассматривают как подмножества множества 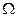, а именно:

.

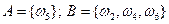Опишем следующие события: .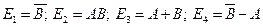

Событие 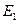состоит в том, что B не произошло, значит

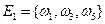={выпало нечетное число очков };

Событие 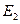состоит в том, что A и B произошли одновременно, значит

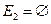- невозможное событие, т.к. число 5 не является четным. Это означает, что события A и B несовместные.

Событие 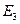состоит в том, что произошло хотя бы одно из событий A или B, значит 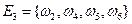={выпало четное число очков или пятерка} .

Событие 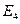состоит в том, что событие 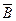произошло, а событие A нет.

Таким образом, 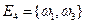={выпали единица или тройка}.