Периодические процессы

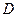Определение.Функция , определенная на множестве , называется периодической если существует такое число 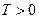, что при каждом 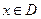, значение 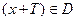и выполняется равенство . Наименьшее из таких чисел называют основным периодом функции.

Простейшими периодическими функциями являются тригонометрические функции и 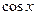. Период этих функций равен 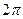, т. е. .

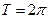Простейшим периодическим процессом (движением) является простое гармоническое колебание (движение), описываемое функцией

, ,

где А – амплитуда колебания, - частота, - начальная фаза.

Функцию такого вида называют простой гармоникой. Основным периодом функции является , т. е. одно полное колебание совершается за промежуток времени 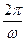( показывает, сколько колебаний совершает точка в течение 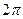единиц времени).

Сложное гармоническое колебание (периодический процесс), возникающее в результате наложения конечного (или бесконечного) числа простых гармоник, также описывается функциями вида и .

Определение.Тригонометрическим рядом называется функциональный ряд вида

,

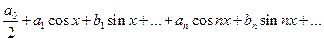
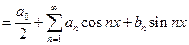действительные числа называются коэффициентами ряда.

Замечание.Тригонометрическийряд можно переписать в виде

.

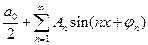Значит, любой периодический процесс, можно задать тригонометрическим рядом, т.е. наложением простых гармоник.

Члены такого ряда удовлетворяют соотношениям (m и n целые положительные числа):

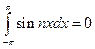при любом n,

.

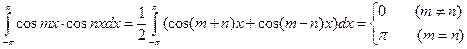
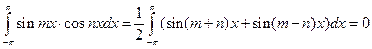
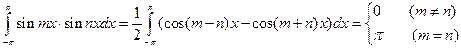Замечание.Приведенные соотношения показывают, что семейство функций 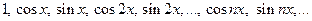обладает свойством ортогональности, т.е.интеграл от произведения любых двух различных функций этого семейства на интервале, имеющем длину 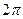, равен нулю.

Будем рассматривать функции 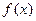, имеющие период 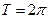. Такие функции называют 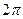- периодическими.

Пусть 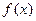- произвольная периодическая функция с периодом 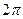. Тогда можно построить тригонометрический ряд на отрезке 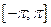следующим образом:

,

где , , .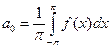

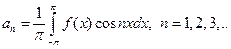Определение.Числа , определяемые по данным формулам, называются коэффициентами Фурье функции 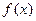, а тригонометрический ряд с такими коэффициентами – рядом Фурье функции 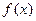; при этом говорят: функции 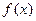соответствует (поставлен в соответствие) ее ряд Фурье.