Ряды Тейлора и Маклорена. Предположим, что функция в промежутке имеет непрерывные производные всех порядков

Предположим, что функция 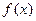в промежутке 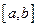имеет непрерывные производные всех порядков. Для такой функции справедливы формулы:

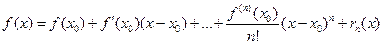
и 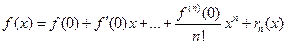, называемые формулами Тейлора и Маклорена. Слагаемое называют остаточным членом формулы.

Составим ряд

,

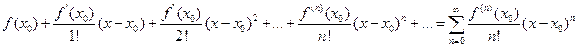в частности, при 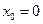, - ряд .

Определение.Такие ряды (независимо от того, сходятся они или нет) называются соответственно рядами Тейлора и рядами Маклорена для функции f(x).

Рассмотрим ряд Маклорена для функции f(x). Этот ряд является степенным, поэтому его область сходимости – интервал .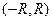

Теорема 7 (Сходимость ряда Маклорена).Для того, чтобы ряд Маклорена сходился и имел своей суммой функцию f(x), необходимо и достаточно, чтобы на 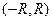остаточный член формулы Маклорена стремился к нулю при : .

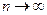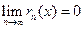Если выполняются условия теоремы, то говорят, что функция 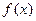разлагается в степенной ряд на интервале .

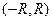Приведем разложение в ряд Маклорена основных элементарных функций и область сходимости рядов:

; ; ;

, ; ;

.

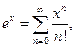
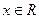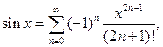
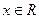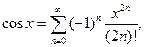
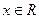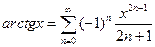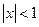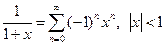Ряды Фурье

Тригонометрический ряд Фурье. Периодические функции.