Оценка остаточного члена в формуле Тейлора
Неотъемлемой частью использования формулы Тейлора является оценка ее остаточного члена. Красивые и практичные формулы появлялись в работах выдающихся математиков 18, 19 и да в 20 веках. Отметим некоторые результаты без доказательства.
Теорема 1(5). (Теорема Лагранжа) Пусть функция 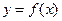 имеет в некоторой окрестности точки
имеет в некоторой окрестности точки 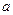 производную
производную 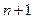 -го порядка. Тогда для произвольной точки
-го порядка. Тогда для произвольной точки 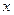 из этой окрестности найдется точка
из этой окрестности найдется точка 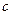 , принадлежащая интервалу, соединяющую точки
, принадлежащая интервалу, соединяющую точки 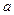 и
и 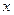 , обладающую тем свойством, что в формуле (5) выполнено соотношение
, обладающую тем свойством, что в формуле (5) выполнено соотношение 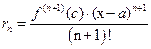 , (13)
, (13)
Теорема 2(6). (Теорема Коши) Пусть функция 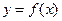 имеет в некоторой окрестности точки
имеет в некоторой окрестности точки 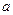 производную
производную 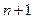 -го порядка. Тогда для произвольной точки
-го порядка. Тогда для произвольной точки 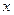 из этой окрестности найдется точка
из этой окрестности найдется точка 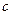 , принадлежащая интервалу, соединяющую точки
, принадлежащая интервалу, соединяющую точки 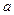 и
и 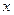 , обладающую тем свойством, что в формуле (5) выполнено соотношение
, обладающую тем свойством, что в формуле (5) выполнено соотношение 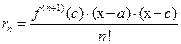 , (14)
, (14)
Теорема 3(5). (Теорема Пеано) Пусть функция 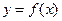 имеет в некоторой окрестности точки
имеет в некоторой окрестности точки 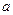 производную
производную 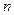 -го порядка. Тогда в формуле (5) выполнено соотношение
-го порядка. Тогда в формуле (5) выполнено соотношение 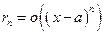 , (15)
, (15)
Так как производные функции 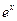 равны между собой и ограничены на любом фиксированном отрезке
равны между собой и ограничены на любом фиксированном отрезке 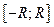 , то остаточный член
, то остаточный член 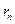 в формуле
в формуле 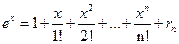 стремится к нулю при
стремится к нулю при 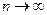 для каждого фиксированного
для каждого фиксированного 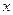 .
.
Тем более то же самое справедливо для функций 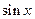 и
и 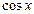 , так как производные этих функций не превосходят по модулю 1. В формулах
, так как производные этих функций не превосходят по модулю 1. В формулах 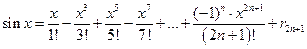 и
и 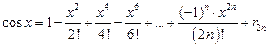 остаточный член стремится к нулю при
остаточный член стремится к нулю при 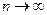 для каждого
для каждого 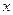 .
.
Можно доказать, что в формуле 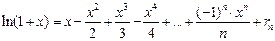 остаточный член стремится к нулю при
остаточный член стремится к нулю при 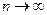 для каждого
для каждого 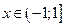 . Посмотрите, как выглядит эта формула при
. Посмотрите, как выглядит эта формула при 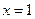 .
.
Дата добавления: 2015-12-10; просмотров: 1486;
