Сходимость функционального ряда
Определение. Функциональный ряд 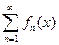 называется сходящимся в точке
называется сходящимся в точке 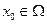 , если сходится соответствующий ему числовой ряд
, если сходится соответствующий ему числовой ряд 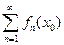 .
.
Определение. Функциональный ряд 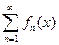 называется сходящимся в области
называется сходящимся в области 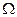 , если он сходится в каждой точке этой области.
, если он сходится в каждой точке этой области.
Определение. Функциональный ряд 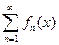 называется абсолютно сходящимся в области
называется абсолютно сходящимся в области 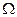 , если в этой области сходится ряд, составленный из модулей его членов, т.е. сходится ряд
, если в этой области сходится ряд, составленный из модулей его членов, т.е. сходится ряд 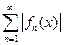 .
.
Определение. Функциональный ряд 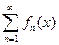 называется условно сходящимся в области
называется условно сходящимся в области 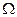 , если он сходится в этой области, а ряд, составленный из модулей его членов, расходится.
, если он сходится в этой области, а ряд, составленный из модулей его членов, расходится.
Определение. Областью сходимости (абсолютной сходимости) функционального ряда 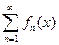 называют множество
называют множество 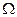 тех значений
тех значений 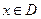 , при которых ряд
, при которых ряд 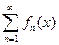 сходится (абсолютно сходится).
сходится (абсолютно сходится).
Пример. Найти область сходимости ряда 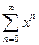 .
.
Решение. Данный ряд является рядом геометрической прогрессии со знаменателем 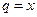 . Следовательно, этот ряд сходится при
. Следовательно, этот ряд сходится при 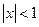 , т.е. при всех
, т.е. при всех 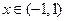 - это область сходимости; сумма ряда равна:
- это область сходимости; сумма ряда равна: 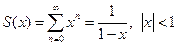 .
.
Пример. Найти область сходимости ряда: 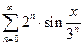 .
.
Решение.Рассмотрим ряд из модулей членов и применим к нему признак Даламбера:
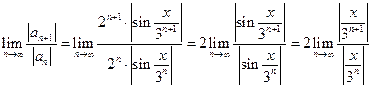 =
= 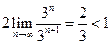 .
.
(Здесь использована эквивалентность бесконечно малых: 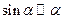 при
при 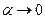 ). Таким образом, ряд абсолютно сходится при любом
). Таким образом, ряд абсолютно сходится при любом 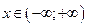 .
.
Дата добавления: 2016-01-09; просмотров: 734;
