Область сходимости степенных рядов
Пусть М – множество всех 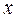 , для которых ряд
, для которых ряд 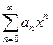 сходится.
сходится.
Определение.Число 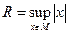 (конечное или бесконечное) называют радиусом сходимости ряда.
(конечное или бесконечное) называют радиусом сходимости ряда.
Если 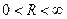 , то для всех
, то для всех 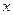 таких, что:
таких, что: 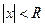 - ряд
- ряд 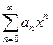 абсолютно сходится, а если
абсолютно сходится, а если 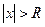 ряд расходится. Если
ряд расходится. Если 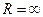 , то ряд абсолютно сходится при всех
, то ряд абсолютно сходится при всех 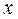 .
.
Радиус сходимости степенного ряда может быть найден по одной из формул: 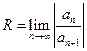 , или
, или 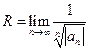 .
.
Пример.Найти область сходимости ряда 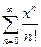 .
.
Решение. В данном случае коэффициенты степенного ряда: 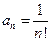 . Воспользуемся формулой
. Воспользуемся формулой
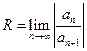 =
= 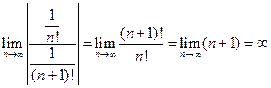 . Отсюда следует, что данный ряд абсолютно сходится на всей числовой оси.
. Отсюда следует, что данный ряд абсолютно сходится на всей числовой оси.
Пример.Найти область сходимости ряда 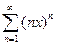 .
.
Решение. 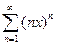 =
= 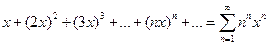 Для определения радиуса сходимости удобно воспользоваться другой формулой:
Для определения радиуса сходимости удобно воспользоваться другой формулой: 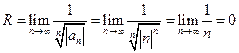 . Значит, ряд сходится только в точке
. Значит, ряд сходится только в точке 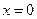 и расходится при всех
и расходится при всех 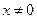 .
.
Пример.Найти область сходимости ряда 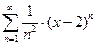 .
.
Решение. 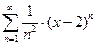 =
= 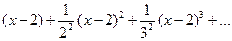 .
.
Применим признак Даламбера к ряду из модулей членов функционального ряда .
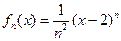 ;
;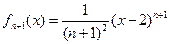 ;
;
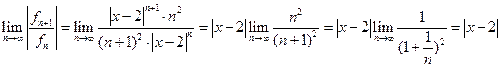 .
.
Тогда, при 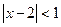 ряд сходится, т.е. область сходимости:
ряд сходится, т.е. область сходимости: 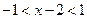 ,
, 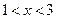 , есть интервал -
, есть интервал - 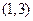 .
.
Если 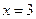 , имеем ряд
, имеем ряд 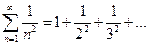 . Этот ряд сходится как обобщеный гармонический
. Этот ряд сходится как обобщеный гармонический 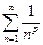 при
при 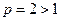 .
.
Если 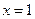 , получаем ряд
, получаем ряд 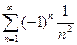 . Этот ряд сходится, так как сходится ряд
. Этот ряд сходится, так как сходится ряд 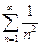 . Значит, исходный ряд сходится при
. Значит, исходный ряд сходится при 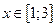 .
.
Дата добавления: 2016-01-09; просмотров: 851;
