Сходимость рядов с произвольными членами

Рассмотрим вещественные знакопеременные ряды, имеющие бесконечно много как положительных, так и отрицательных членов.

Примерызнакопеременных рядов:

1) ;

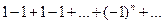2) 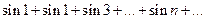-этот ряд является знакопеременным, так как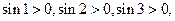 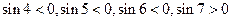, и т. д.

Частным случаем знакопеременных рядов являются знакочередующиеся ряды:

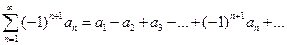, где

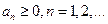
Теорема 10 (Признак Лейбница).Пусть в ряде 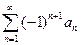числа 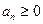такие, что 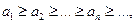и 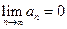. Тогда этот ряд сходится.

Рассмотрим произвольный числовой ряд с вещественными или комплексными членами и положительный ряд, составленный из модулей .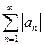

Определение. Ряд называют абсолютно сходящимся, если сходится ряд .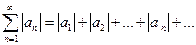

Определение. Ряд называют условно сходящимся, если он сходится, а ряд 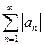расходится.

Теорема 11.Если сходится ряд 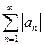, то сходится и ряд .

Для исследования абсолютной сходимости можно использовать признаки сходимости рядов с положительными членами (например, Даламбера и Коши).

Пример.Исследовать сходимость знакопеременного ряда (абсолютную и условную сходимость): .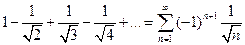

Решение.Рассмотрим ряд, составленный из абсолютных величин данного ряда: 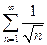. Этот ряд расходится, как обобщенный гармонический ряд 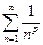при 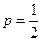. Исходный ряд знакочередующийся, его члены монотонно убывают по абсолютной величине и 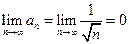. Следовательно, он сходится по признаку Лейбница. Значит, сходимость этого ряда условная.

Пример. Исследовать сходимость знакопеременного ряда: .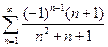

Решение. Рассмотрим положительный ряд: 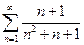. Используя предельный признак сравнения, сравним этот ряд с гармоническим рядом 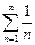: 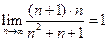. Таким образом, ряд 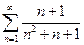расходится. Исходный ряд знакочередующийся, его члены монотонно убывают по абсолютной величине, и 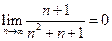. Значит, он сходится по признаку Лейбница. Значит, исходный ряд сходится условно.