Теорема Коши. Вычисление интегралов от аналитических функций
Мы уже отмечали, что условия, при выполнении которых функция 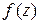 является аналитической, достаточно жесткие. Это и обуславливает справедливость следующей теоремы.
является аналитической, достаточно жесткие. Это и обуславливает справедливость следующей теоремы.
Теорема 2 (Теорема Коши).Если 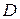 - односвязная область комплексной плоскости и
- односвязная область комплексной плоскости и 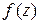 - однозначная аналитическая в этой области функция, то для любой замкнутой спрямляемой кривой
- однозначная аналитическая в этой области функция, то для любой замкнутой спрямляемой кривой 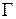 , лежащей в области
, лежащей в области 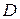 , интеграл от
, интеграл от 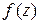 вдоль
вдоль 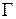 равен нулю:
равен нулю: 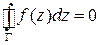 .
.
Отметим, что теорема Коши остается справедливой и для многосвязной области.
Из теоремы 2 вытекает, что интегралы от аналитической функции вдоль любых двух кривых  и
и 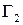 с общим началом
с общим началом 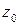 и концом
и концом 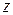 имеют равные значения.
имеют равные значения.
В самом деле, кривая 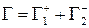 является замкнутой, и, следовательно,
является замкнутой, и, следовательно,
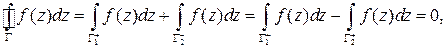 откуда
откуда

Это означает, что интеграл от функции 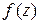 , аналитической в односвязной области
, аналитической в односвязной области 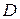 , не зависит от кривой
, не зависит от кривой 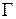 (от пути интегрирования), а зависит только от начальной и конечной точек этой кривой. Поэтому для интеграла вдоль произвольной спрямляемой кривой
(от пути интегрирования), а зависит только от начальной и конечной точек этой кривой. Поэтому для интеграла вдоль произвольной спрямляемой кривой 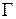 , соединяющей точки
, соединяющей точки 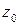 и
и 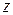 , можно пользоваться обозначением
, можно пользоваться обозначением 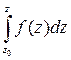 .
.
Рассмотрим интеграл от аналитической функции, если конечная точка – переменная, т.е. 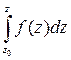 есть некоторая функция от верхнего предела:
есть некоторая функция от верхнего предела:
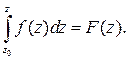
Можно показать, что 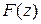 - аналитическая функция, и что ее производная равна
- аналитическая функция, и что ее производная равна 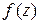 . Таким образом, интеграл
. Таким образом, интеграл 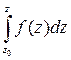 является первообразной для подынтегральной функции (определение первообразной аналитической функции аналогично определению первообразной функции действительной переменной).
является первообразной для подынтегральной функции (определение первообразной аналитической функции аналогично определению первообразной функции действительной переменной).
И это позволяет сделать вывод о справедливости формулы Ньютона-Лейбница:
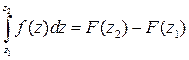 ,
,
здесь 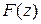 - одна из первообразных функции
- одна из первообразных функции 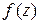 , (
, ( 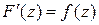 ).
).
Этот результат позволяет сводить вычисление интеграла от аналитической функции 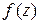 к отысканию какой-либо первообразной функции и, следовательно, использовать известные формулы и методы интегрирования функций действительной переменной. В частности, если
к отысканию какой-либо первообразной функции и, следовательно, использовать известные формулы и методы интегрирования функций действительной переменной. В частности, если 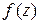 и
и 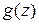 аналитические функции, то будет справедлива формула интегрирования по частям:
аналитические функции, то будет справедлива формула интегрирования по частям:
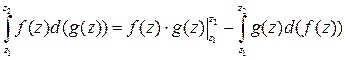 .
.
Пример. Вычислить интеграл 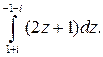
Решение. Подынтегральная функция является аналитической на всей комплексной плоскости, поэтому для нее существует первообразная. Воспользуемся формулой Ньютона-Лейбница:

Пример.Вычислить интеграл 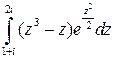 .
.
Решение. Подынтегральная функция является аналитической, поэтому воспользуемся формулой интегрирования по частям:
 =
= 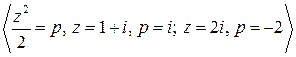 =
=
= 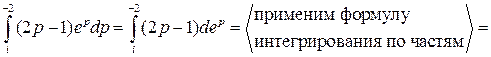
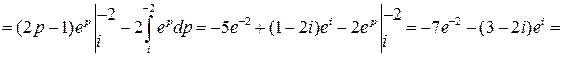
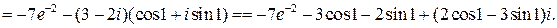
Аналитические функции комплексного переменного обладают следующим замечательным свойством:
Теорема 3. (Интегральная формула Коши)Если 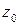 - внутренняя точка односвязной области
- внутренняя точка односвязной области 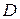 , ограниченной замкнутым контуром
, ограниченной замкнутым контуром 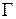 ,
, 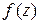 - аналитическая в замкнутой области
- аналитическая в замкнутой области 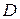 функция, то справедлива формула:
функция, то справедлива формула:

Иными словами, если мы знаем значение аналитической функции на границе односвязной области, то мы можем найти значение этой функции в любой внутренней точке области.
Более того, справедлива следующая теорема.
Теорема 4.Если однозначная функция комплексного переменного 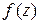 имеет всюду в области
имеет всюду в области 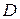 первую производную, то она имеет в этой области и все производные высших порядков, которые могут быть найдены по формуле:
первую производную, то она имеет в этой области и все производные высших порядков, которые могут быть найдены по формуле:
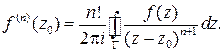
Интегральную формулу Коши и формулу для производных высших порядков можно использовать для вычисления интегралов по замкнутому контуру.
Пример. Вычислить интеграл 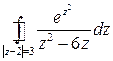 .
.
Решение. Рассмотрим подынтегральную функцию 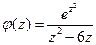 . Аналитичность этой функции нарушается в точках:
. Аналитичность этой функции нарушается в точках: 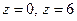 (точки, в которых знаменатель равен 0). Контур, по которому вычисляется интеграл:
(точки, в которых знаменатель равен 0). Контур, по которому вычисляется интеграл: 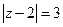 , есть окружность с центром в точке
, есть окружность с центром в точке 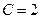 и радиусом 3. Внутри этого контура лежит точка
и радиусом 3. Внутри этого контура лежит точка 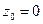 , поэтому внутри контура подынтегральная функция не является аналитической. Запишем эту функцию в виде:
, поэтому внутри контура подынтегральная функция не является аналитической. Запишем эту функцию в виде: 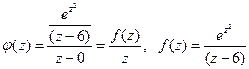 . Тогда функция
. Тогда функция 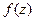 является аналитической внутри замкнутого контура. Воспользуемся интегральной формулой Коши:
является аналитической внутри замкнутого контура. Воспользуемся интегральной формулой Коши:
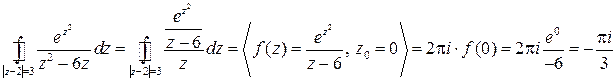 .
.
Пример. Вычислить интеграл  .
.
Решение. Аналитичность подынтегральной функции нарушается в точках 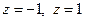 . Внутри контура есть только одна из них:
. Внутри контура есть только одна из них: 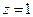 . Преобразуем подынтегральную функцию к виду:
. Преобразуем подынтегральную функцию к виду:
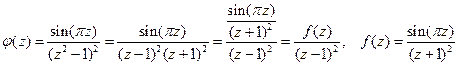 .
.
Функция 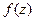 - аналитическая внутри контура, поэтому можно применить теорему 4 (в данном случае
- аналитическая внутри контура, поэтому можно применить теорему 4 (в данном случае  ):
):

Теория рядов
2.1. Числовые ряды
Основные понятия
Пусть дана последовательность чисел (вещественных или комплексных) 
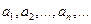
Определение. Выражение 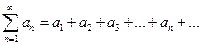 называют числовым рядом, или просто рядом, а сами числа
называют числовым рядом, или просто рядом, а сами числа 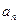 - членами ряда.
- членами ряда.
Числовой ряд будем обозначать  .
.
Ряд считается заданным, если известен общий член ряда 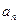 , выраженный как функция его номера n:
, выраженный как функция его номера n: 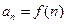 .
.
Определение. Сумма первых n членов ряда 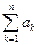 называется n-й частичной суммой ряда и обозначается
называется n-й частичной суммой ряда и обозначается 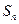 , т.е.
, т.е. 
Рассмотрим частичные суммы:
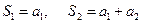 ,…,
,…, 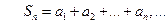
Определение. Если последовательность 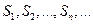 имеет конечный предел:
имеет конечный предел: 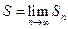 , то говорят, что ряд
, то говорят, что ряд  сходится. В этом случае, предел
сходится. В этом случае, предел 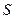 называют суммой ряда и пишут:
называют суммой ряда и пишут: 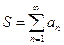 .
.
Ряд  расходится, если последовательность
расходится, если последовательность 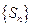 не имеет предела или он равен
не имеет предела или он равен 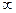 . Если
. Если 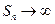 , то говорят, что сумма ряда равна
, то говорят, что сумма ряда равна 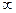 , и пишут:
, и пишут: 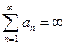 .
.
Пример.Показать, что числовой ряд 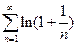 расходится.
расходится.
Решение. Запишем n-ю частичную сумму ряда. Имеем 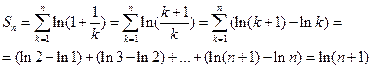
Тогда при 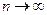 имеем
имеем 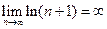 . Следовательно, ряд расходится, и считается,что его сумма равна
. Следовательно, ряд расходится, и считается,что его сумма равна 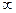 .
.
Пример. Показать, что ряд 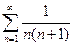 сходится.
сходится.
Решение. Частичные суммы ряда имеют вид: 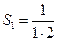 ,
, 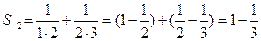 , …,
, …, 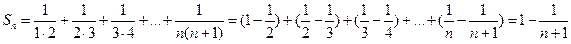 . Вычислим сумму ряда:
. Вычислим сумму ряда: 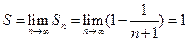 , т.е. ряд сходится, и его сумма равна 1.
, т.е. ряд сходится, и его сумма равна 1.
Пример.Исследовать на сходимость ряд, члены которого образуют геометрическую прогрессию: 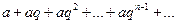 =
= 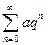
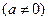 .
.
Решение.Сумма первых n членов прогрессии вычисляется по формуле 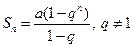 . Найдем предел этой суммы:
. Найдем предел этой суммы: 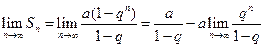 .
.
В зависимости от величины q имеем:
1) если 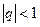 , то
, то 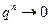 при
при  . Поэтому
. Поэтому 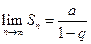 , ряд сходится, его сумма равна
, ряд сходится, его сумма равна 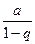 ;
;
2) если 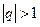 , то
, то  при
при  . Поэтому
. Поэтому 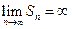 , ряд расходится;
, ряд расходится;
3) если 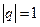 , то при
, то при 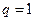 ряд принимает вид
ряд принимает вид  ,
,
для него 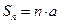 и
и 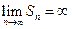 , т.е. он расходится;
, т.е. он расходится;
при 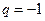 ряд принимает вид
ряд принимает вид 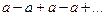 , в этом случае
, в этом случае 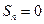 при четном n и
при четном n и 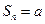 при нечетном n. Следовательно,
при нечетном n. Следовательно, 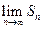 не существует, ряд расходится.
не существует, ряд расходится.
Таким образом, ряд сходится при 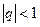 и расходится при
и расходится при 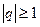 . Такой ряд будем называть рядом геометрической прогрессии.
. Такой ряд будем называть рядом геометрической прогрессии.
Дата добавления: 2016-01-09; просмотров: 8722;
