Определение интеграла от функции комплексного переменного
Пусть на комплексной плоскости задана ориентированная кусочно-гладкая кривая 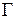 , вдоль которой определена функция
, вдоль которой определена функция 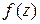 .
.
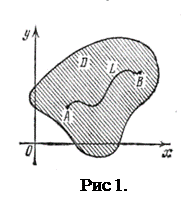
Замечание. Дуга называется гладкой, если она может быть задана непрерывно-дифференцируемой функцией. Кривая, состоящая из конечного числа гладких дуг, называется кусочно – гладкой.
Разобьем эту кривую на 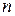 частей
частей 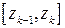 точками
точками 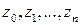 , пронумерованными в направлении от
, пронумерованными в направлении от 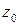 - начальной точки кривой
- начальной точки кривой 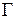 , до
, до 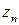 - конечной точки
- конечной точки 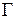 . Обозначим через
. Обозначим через 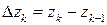 (
( 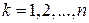 ). В каждой части выберем произвольно точку
). В каждой части выберем произвольно точку 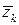 (
( 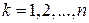 ) и составим сумму:
) и составим сумму:
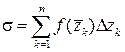 ,
,
которую назовем интегральной суммой.
Устремим 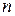 в бесконечность так, чтобы
в бесконечность так, чтобы 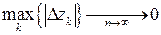 .
.
Определение. Если существует предел интегральной суммы 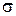 при условии произвольного способа разбиения кривой
при условии произвольного способа разбиения кривой 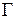 на части, произвольного выбора точек
на части, произвольного выбора точек 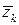 (
( 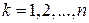 ) и при условии
) и при условии 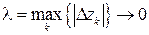 , то этот предел называется интегралом от функции
, то этот предел называется интегралом от функции 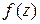 по дуге (контуру)
по дуге (контуру) 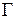 и обозначается:
и обозначается:
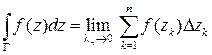 .
.
Из определения интеграла следует, что его значения зависят не только от функции 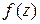 , но и от пути интегрирования Г. Если кривая
, но и от пути интегрирования Г. Если кривая 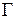 замкнутая (точки
замкнутая (точки 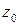 и
и 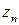 совпадают), то интеграл обозначают символом:
совпадают), то интеграл обозначают символом: 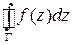 .
.
Если функция 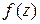 непрерывна вдоль кривой
непрерывна вдоль кривой 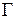 , то интеграл
, то интеграл 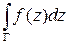 существует.
существует.
Пусть 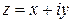 и
и 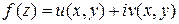 ,
,
тогда 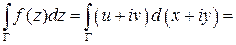
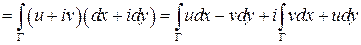 .
.
Таким образом, интеграл от функции комплексного переменного равен сумме двух криволинейных интегралов 2-го рода от вещественных функций:
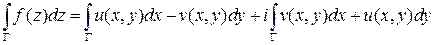 .
.
Если кривая 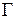 задана параметрическим уравнением:
задана параметрическим уравнением:
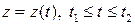 (или
(или 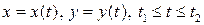 ), тогда:
), тогда:
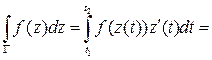
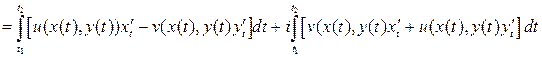 .
.
Замечание. Довольно часто в качестве параметра 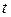 выбирают угол:
выбирают угол: 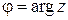 .
.
Поскольку интеграл от функции комплексного переменного сводится к криволинейным интегралам второго рода от действительных функций, то его свойства будут аналогичны известным свойствам криволинейных интегралов:
· 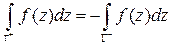 ,
,
где 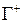 и
и 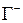 - один и тот же контур, проходимый в положительном и отрицательном направлениях (в качестве положительного направления обхода замкнутого контура принимается направление, при котором внутренняя область, ограниченная данным замкнутым контуром, остается слева от направления движения).
- один и тот же контур, проходимый в положительном и отрицательном направлениях (в качестве положительного направления обхода замкнутого контура принимается направление, при котором внутренняя область, ограниченная данным замкнутым контуром, остается слева от направления движения).
· 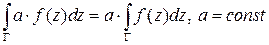 .
.
· 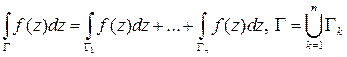 .
.
· 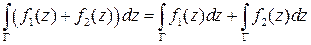 .
.
· Если вдоль кривой 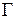 :
: 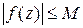 , и длина кривой
, и длина кривой 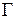 есть
есть 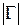 , то
, то 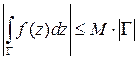 .
.
· 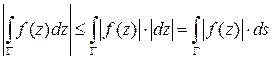 ,
, 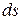 - дифференциал длины дуги.
- дифференциал длины дуги.
Пример. Вычислить интеграл 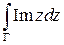 , где
, где 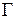 - дуга параболы
- дуга параболы 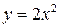 от точки 0 до точки
от точки 0 до точки 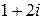 .
.
Решение. Так как для всех точек кривой 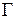 имеем:
имеем: 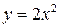 , то
, то 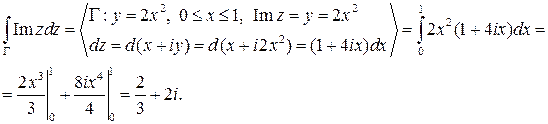
Пример. Вычислить интеграл 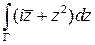 , где
, где 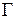 - часть окружности
- часть окружности 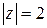 ,
, 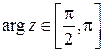 .
.
Решение. 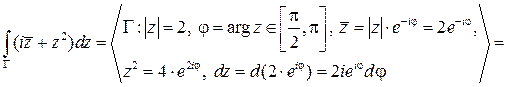
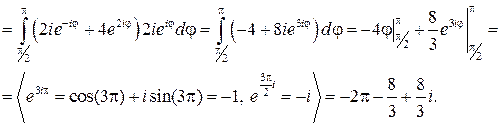
Дата добавления: 2016-01-09; просмотров: 1714;
