Гиперболические функции
Гиперболические функции 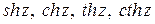 определяются равенствами:
определяются равенствами: 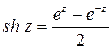 - гиперболический синус (
- гиперболический синус ( 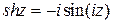 ),
),
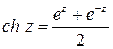 - гиперболический косинус (
- гиперболический косинус ( 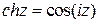 ),
),
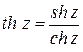 - гиперболический тангенс,
- гиперболический тангенс,
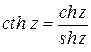 - гиперболический котангенс.
- гиперболический котангенс.
Свойства гиперболических функций вытекают из свойств функций 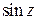 и
и 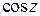 ; все формулы, справедливые при действительных значениях x, остаются справедливыми и для комплексных значений z.
; все формулы, справедливые при действительных значениях x, остаются справедливыми и для комплексных значений z.
Логарифмическая функция
Логарифмическая функция 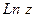 определяется как функция обратная к показательной.
определяется как функция обратная к показательной.
Определение.Если 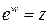 , где
, где 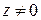 , то
, то 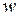 называется логарифмом числа
называется логарифмом числа
z и обозначается 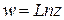
Перепишем равенство 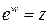 в виде
в виде 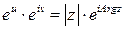 , тогда получим, что
, тогда получим, что 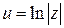 и
и 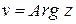 .
.
Следовательно, логарифмическая функция задается равенством:
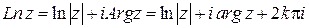 ,
, 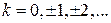

Логарифмическая функция многозначна; ее ветвь, соответствующую главному значению аргумента 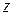 , называют главным значением логарифмической функции и обозначают
, называют главным значением логарифмической функции и обозначают 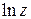 . Таким образом,
. Таким образом,
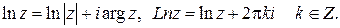
Свойства логарифмической функции:
· 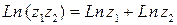
· 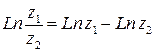
· 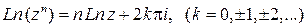
· 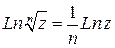 .
.
Обратные тригонометрические функции
Определение.Если 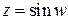 , то
, то 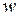 называется арксинусом числа z и обозначается
называется арксинусом числа z и обозначается 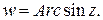
Разрешая уравнение 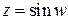 относительно
относительно 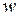 , получим:
, получим:
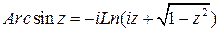 .
.
Аналогично можно получить выражения для других обратных тригонометрических функций; все они выражаются через логарифмическую функцию:
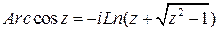 ,
, 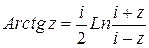 ,
, 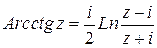 .
.
Пример. Найти 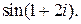
Решение. 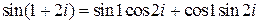 , но
, но 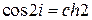 ,
, 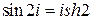 и поэтому
и поэтому 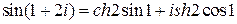 .
.
Пример. Найти: а) 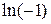 , б)
, б) 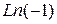
Решение. а) Поскольку 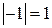 , а главное значение аргумента у числа -1 равно
, а главное значение аргумента у числа -1 равно 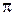 , то получим:
, то получим: 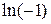 =
= 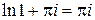 .
.
б) по формуле 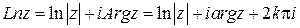 получаем
получаем 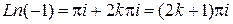
Пример. Найти 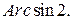
Решение. По определению функции 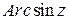 получаем:
получаем:
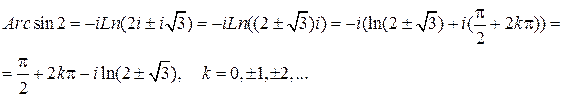
Пример.Записать в алгебраической форме 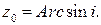
Решение. 
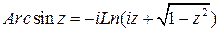 , тогда имеем
, тогда имеем
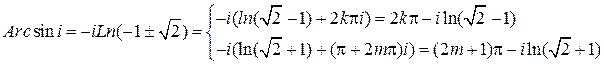
Дата добавления: 2016-01-09; просмотров: 800;
