Определение комплексного числа

Теория функций комплексного переменного

Комплексные числа и операции над ними

Определение комплексного числа

Определение.Комплексным числом z называется упорядоченная пара действительных чисел : .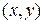

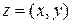Например: , .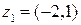

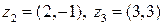Действительные числа х и у называются, соответственно, действительной и мнимой частями комплексного числа z и обозначаются: .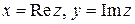

Комплексные числа, у которых мнимая часть равна нулю, т.е. числа вида: 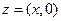отождествляют с действительными числами.

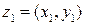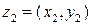Определение.Два комплексных числа и называются равными тогда и только тогда, когда 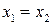и 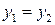, то есть

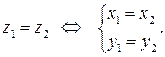
Определение.Суммойкомплексных чисел 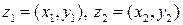называется комплексное число z, определяемое равенством:

.

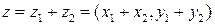Определение.Произведением комплексных чисел 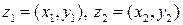называется комплексное число z, определяемое равенством:

.

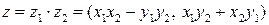Геометрически комплексное число 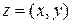можно изобразить точкой 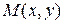на плоскости, т.е. точкой с декартовыми координатами 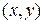, или вектором 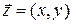, идущим из начала координат в точку 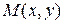(радиус-вектором точки М). Плоскость, на которой комплексные числа изображаются как точки, называется комплексной плоскостью. Ось 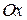называется вещественной осью, ось 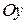называется мнимой осью. Масштабная единица оси 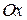, т.е. комплексное число 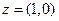есть вещественная единица; масштабная единица оси 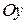, т.е. число 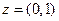называется мнимой единицей, это число имеет специальное обозначение .

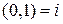По правилу умножения комплексных чисел получим: .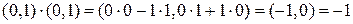

Таким образом, 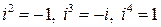и т.д.

Комплексные числа вида: 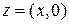изображаются точками на оси 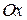и являются вещественными числами (множество вещественных или действительных чисел есть подмножество множества комплексных чисел). Комплексные числа вида 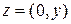изображаются точками на оси 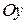и называются чисто мнимыми числами.

Определение.Вещественное неотрицательное число:

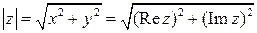
называют модулем комплексного числа .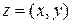

Геометрически, модуль комплексного числа – это расстояние от точки, изображающей число до начала координат (или длина радиус-вектора точки).

Определение.Угол 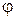между положительным направлением оси 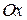и вектором 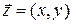называют аргументом комплексного числа .

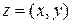Этот угол определен неоднозначно, с точностью до 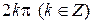; его обозначают 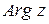и называют общим значением аргумента.

Главным значением аргумента комплексного числа называют значение угла 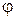, заключенное в промежутке длины 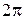, его обозначают 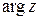. Будем считать, что .

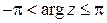Общее значение аргумента и главное значение связаны соотношением: 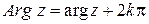, к=0,1,-1,2,-2,….

Из определения модуля и аргумента следует, что, если 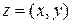, то

,

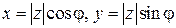и для вычисления 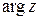получаем формулы:

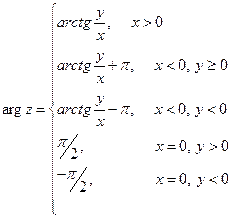
Справедливы следующие свойства модуля и аргумента комплексного числа:

·

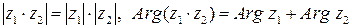
(при перемножении комплексных чисел их модули перемножаются, а аргументы складываются);

·

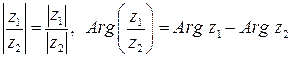
(модуль частного двух комплексных чисел есть частное модулей, а аргумент – разность аргументов делимого и делителя).