Производные основных элементарных функций
· Показательная функция 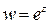 .
.
Имеем 
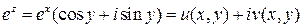 .
.
Действительная и мнимая части 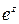 будут, соответственно,
будут, соответственно,
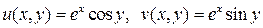 .
.
Находим частные производные: 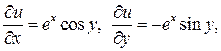
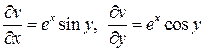 . Следовательно,
. Следовательно, 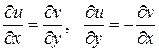 , т.е. условия Коши-Римана выполнены, значит, функция
, т.е. условия Коши-Римана выполнены, значит, функция 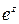 аналитическая, и ее производная:
аналитическая, и ее производная:
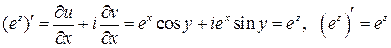 .
.
· Функция 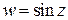 .
.
По определению: 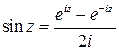 . Т.е. является аналитической функцией, тогда, пользуясь правилами дифференцирования, получим:
. Т.е. является аналитической функцией, тогда, пользуясь правилами дифференцирования, получим:
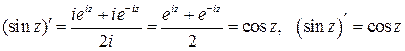 .
.
· Функция 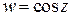 .
.
Аналогично предыдущему:
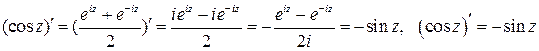 .
.
· Функция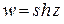 .
.
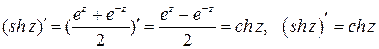 .
.
· Функция 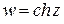 .
.
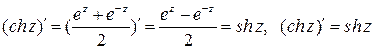 .
.
· Функция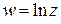 .
.
Логарифмическая функция является обратной к показательной функции, а значит – аналитической. Воспользуемся правилом дифференцирования обратной функции.
Имеем: 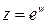 , тогда
, тогда
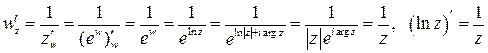 .
.
· Функция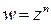 .
.
Производную степенной функции вычислим непосредственно по определению:
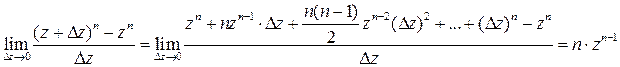 .Предел существует, следовательно, функция
.Предел существует, следовательно, функция 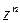 аналитическая, и ее производная:
аналитическая, и ее производная:
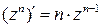 .
.
Таким образом, мы показали, что основные элементарные функции комплексного переменного являются аналитическими функциями. Следовательно, всякая функция комплексного переменного, являющаяся композицией конечного числа основных элементарных функций, будет аналитической или дифференцируемой в области своего определения.
Пример.Вычислить производную функции 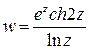 .
.
Решение. Имеем: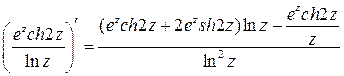 =
=
= 
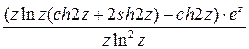 .
.
1.3.4. Восстановление аналитической функции по известной действительной или мнимой части
Условия, при которых функция комплексного переменного дифференцируема, достаточно жесткие. Поэтому, аналитическая функция, с точностью до постоянного слагаемого, может быть задана свой действительной или мнимой частью.
Действительная и мнимая части функции 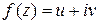 , аналитической в некоторой области D, связаны условиями Коши – Римана:
, аналитической в некоторой области D, связаны условиями Коши – Римана:
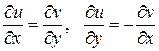 .
.
Пусть известна одна из частей аналитической функции, например 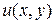 . Из условия:
. Из условия: 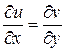 можно найти
можно найти 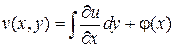 (с точностью до неизвестной функции
(с точностью до неизвестной функции 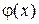 ). Эту функцию
). Эту функцию 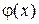 , с точностью до постоянного слагаемого, найдем из второго условия
, с точностью до постоянного слагаемого, найдем из второго условия 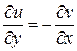 .
.
А именно, 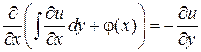 или
или 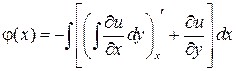 .
.
Пример.Найти аналитическую функцию 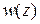 , если известна её мнимая часть
, если известна её мнимая часть 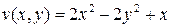 .
.
Решение. Так как 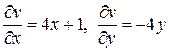 , то из условия
, то из условия 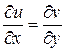 находим:
находим: 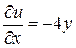 . Следовательно,
. Следовательно, 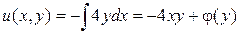 , где функция
, где функция 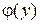 пока неизвестна. Для нахождения функции
пока неизвестна. Для нахождения функции 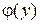 дифференцируем это равенство по y и приравниваем к известной производной, используя условие
дифференцируем это равенство по y и приравниваем к известной производной, используя условие 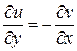 :
:
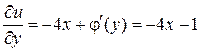 , откуда
, откуда 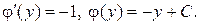
Следовательно, 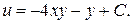 Окончательно получаем
Окончательно получаем
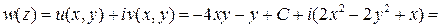
= 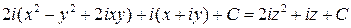 .
.
Ответ. 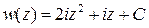 .
.
Дата добавления: 2016-01-09; просмотров: 749;
